Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 671234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666869707172737475767778798081828384858687888990919293949596979899100

Enunciado

James Stewart – Cálculo Volume 2 – Tradução da 7ª edição americana. Capítulo 15 Seção 4 Problema 9.

(Cap 15.4 – Ex 9) Calcule a integral dada, colocando-a em coordenadas polares.

∬ R sen ⁡ x 2 + y 2 d A

Onde R é a região do primeiro quadrante entre os círculos com centro a origem e raios 1 e 3.

Passo 1

Falaiii galerinha, show de bolinhas?

Sabemos que ...

Inicialmente precisamos mudar a função de integração de coordenadas cartesianas para coordenadas polares. Portanto, temos:

∬ R sen ⁡ x 2 + y 2 d A = ∬ R r sen ⁡ r 2 d A

Agora, precisamos escrever a nossa região em coordenadas polares. O valor do raio r varia de 1 até 3 (região entre os círculos), e o valor de θ varia de 0 até π / 2 , equivalente ao primeiro quadrante.

Considerando a integral dada, temos

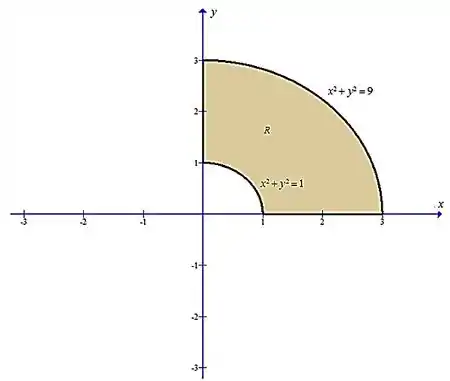
A região R

Passo 2

Agora que descrevemos a região em coordenadas polares, podemos colocar os limites de integração na nossa integral. Portanto,

∫ 0 π / 2 ∫ 1 3 r sen ⁡ r 2 d r d θ

Resolvendo a integral de dentro, por substituição:

u = r 2 → d u = 2 r   d r

∫ sen ⁡ u d u 2 = - cos ⁡ u 2

= - cos ⁡ r 2 2

Voltando:

∫ 0 π 2 - cos ⁡ r 2 2 1 3 d θ

= ∫ 0 π / 2 - cos ⁡ 9 2 + cos ⁡ 1 2 d θ    

= π cos ⁡ 1 - cos ⁡ 9 4

Resposta

∬ R sen ⁡ x 2 + y 2 d A = π cos ⁡ 1 - cos ⁡ 9 4

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}