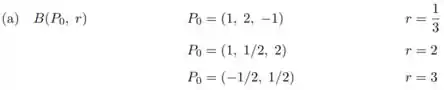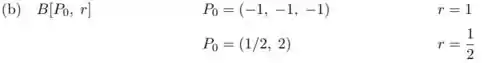Listas de Cáclulo 2 - Profº Félix Gómez de Cálculo Diferencial e Integral 2 da UTFPR - Primeira Lista
Cálculo Diferencial e Integral 2 - UTFPR
Identificar as afirmações verdadeiras
A união de bolas abertas é uma bola aberta.
Ver solução completaIdentificar as afirmações verdadeiras
c A união de bolas abertas é um conjunto conexo.
Ver solução completaSeja a função, e o conjunto
Resolva as questões,
a seguir trace um esboço mostrando como um sólido sombreado em , o conjunto de pontos do domínio de .
Ver solução completaEncontre o domínio e a imagem da função e trace um esboço mostrando uma região sombreada em , como um conjunto de pontos no domínio de .
Ver solução completaEncontre o domínio e a imagem da função e trace um esboço mostrando uma região sombreada em , como um conjunto de pontos no domínio de .
Ver solução completaEncontre o domínio e a imagem da função e trace um esboço mostrando uma região sombreada em , como um conjunto de pontos no domínio de .
Ver solução completaDetermine a região de continuidade de e trace o esboço, mostrando com uma região sombreada em a região de continuidade de :
a)
Ver solução completaDetermine a região de continuidade de e trace o esboço, mostrando com uma região sombreada em a região de continuidade de :
b)
Ver solução completaDetermine a região de continuidade de e trace o esboço, mostrando com uma região sombreada em a região de continuidade de :
c)
Ver solução completaDetermine a região de continuidade de e trace o esboço, mostrando com uma região sombreada em a região de continuidade de :
d)
Ver solução completaMostre que a função é descontínua na origem. Depois determine se a continuidade é removível ou essencial. Se a descontinuidade for removível defina tal que remova a descontinuidade.
a)
Ver solução completaMostre que a função é descontínua na origem. Depois determine se a continuidade é removível ou essencial. Se a descontinuidade for removível defina tal que remova a descontinuidade.
b)
Ver solução completaMostre que a função é descontínua na origem. Depois determine se a continuidade é removível ou essencial. Se a descontinuidade for removível defina tal que remova a descontinuidade.
c)
Ver solução completaMostre que a função é descontínua na origem. Depois determine se a continuidade é removível ou essencial. Se a descontinuidade for removível defina tal que remova a descontinuidade.
d)
Ver solução completaEncontre as derivadas parciais, como se fossem derivadas ordinárias, considerando constantes todas menos uma das variáveis.
(1)
Ver solução completaEncontre as derivadas parciais, como se fossem derivadas ordinárias, considerando constantes todas menos uma das variáveis.
(2)
Ver solução completaEncontre as derivadas parciais, como se fossem derivadas ordinárias, considerando constantes todas menos uma das variáveis.
(3)
Ver solução completaEncontre as derivadas parciais, como se fossem derivadas ordinárias, considerando constantes todas menos uma das variáveis.
(4)
Ver solução completa4] Encontre as derivadas parciais, como se fossem derivadas ordinárias, considerando constantes todas menos uma das variáveis
(5)
Ver solução completa4] Encontre as derivadas parciais, como se fossem derivadas ordinárias, considerando constantes todas menos uma das variáveis
(6)
Ver solução completa4] Encontre as derivadas parciais, como se fossem derivadas ordinárias, considerando constantes todas menos uma das variáveis
(7)
Ver solução completa4] Encontre as derivadas parciais, como se fossem derivadas ordinárias, considerando constantes todas menos uma das variáveis
(8)
Ver solução completa2] Cada uma das seguintes inequações determina um conjunto de pontos em e . Identificar as bolas abertas e as bolas fechadas identificando o centro e seu raio.
(a)
Ver solução completa2] Cada uma das seguintes inequações determina um conjunto de pontos em e . Identificar as bolas abertas e as bolas fechadas identificando o centro e seu raio.
(b)
Ver solução completa2] Cada uma das seguintes inequações determina um conjunto de pontos em e . Identificar as bolas abertas e as bolas fechadas identificando o centro e seu raio.
(c)
Ver solução completa2] Cada uma das seguintes inequações determina um conjunto de pontos em e . Identificar as bolas abertas e as bolas fechadas identificando o centro e seu raio.
(d)
Ver solução completa2] Cada uma das seguintes inequações determina um conjunto de pontos em e . Identificar as bolas abertas e as bolas fechadas identificando o centro e seu raio.
(e)
Ver solução completa2] Cada uma das seguintes inequações determina um conjunto de pontos em e . Identificar as bolas abertas e as bolas fechadas identificando o centro e seu raio.
(f)
Ver solução completaConsidere as seguintes normas,
para
Verifique com um exemplo em que a identidade do paralelogramo não é válida para as normas acima cidadãs.
Ver solução completaEncontre o domínio e a imagem da função e trace um esboço mostrando uma região sombreada em , como um conjunto de pontos no domínio de .
Ver solução completaEncontre o domínio e a imagem da função e trace um esboço mostrando uma região sombreada em , como um conjunto de pontos no domínio de .
Ver solução completaEncontre o domínio e a imagem da função e trace um esboço mostrando uma região sombreada em , como um conjunto de pontos no domínio de .
Ver solução completaEncontre o domínio e a imagem da função e trace um esboço mostrando uma região sombreada em , como um conjunto de pontos no domínio de .
Ver solução completaEncontre o domínio e a imagem da função e trace um esboço mostrando uma região sombreada em , como um conjunto de pontos no domínio de .
Ver solução completaEstabeleça o limite, encontrando para qualquer de maneira que a definição seja
válida.
Ver solução completaEstabeleça o limite, encontrando para qualquer de maneira que a definição seja
válida.
Ver solução completaEstabeleça o limite, encontrando para qualquer de maneira que a definição seja
válida.
Ver solução completaEstabeleça o limite, encontrando para qualquer de maneira que a definição seja
válida.
Ver solução completaEstabeleça o limite, encontrando para qualquer de maneira que a definição seja
válida.
Ver solução completaEstabeleça o limite, encontrando para qualquer de maneira que a definição seja
válida.
Ver solução completa6] Dada a função . Verifique se satisfaz a equação diferencial em derivadas parciais,
Ver solução completa11] Encontre a declividade da reta tangente à curva de interseção da superfície com o plano no ponto . Trace um esboço. Interprete essa declividade como uma derivada parcial
Ver solução completa12] Mostre que a função de duas variáveis é solução do problema de valor inicial e na fronteira,
Ver solução completa13] Mostre que , onde é uma função diferenciável arbitrária, é uma solução geral da equação em derivadas parciais
Ver solução completa14] Mostre que é uma solução geral da equação em derivadas parciais,
Também encontre a solução particular satisfazendo as condições , , .
Ver solução completa16] De acordo com a lei de gases ideais para um gás confinado, Se for a pressão, unidades cúbicas o volume e graus a temperatura, temos
onde é uma constante de proporcionalidade. Mostre que
Ver solução completa17] A temperatura em qualquer ponto de uma placa é graus, e
Se a distância for medida em polegadas, encontre no ponto a taxa de variação da temperatura em relação à distância na placa na direção do eixo positivo e na direção do eixo positivo.
Ver solução completaConsidere a norma do máximo em , então a norma de é dada por
Faça um esboço de uma bola de centro e raio .
Ver solução completaConsidere a norma da soma em , então a norma de é dada por
Faça um esboço de uma bola de centro e raio .
Ver solução completaMostre que toda bola aberta é convexa.
Isto significa que, as bolas relativas a diferentes normas em tem em comum o fato de serem convexas.
Ver solução completaConsidere uma bola de centro arbitrário, contendo um subconjunto de . Mostre que é limitado.
Ver solução completaCom uma simples modificação no exercício anterior, mostre que a bola aberta é um
conjunto aberto para quaisquer
Ver solução completa