Lista de Estudos pra Prova - Stewart Vol 2 - 7°ed de Cálculo Diferencial e Integral 2 da UTFPR - Derivadas Parciais

(Capítulo 14.1 – Exercício 66) Descreva as superfícies de nível da função.

(Cap. 14.1 - Ex. 5) Um modelo para a área da superfície de um corpo humano é dado pela função

onde é o peso (em libras), é a altura (em polegadas) e é medida em pés quadrados.

a) Encontre e interprete-a.

b) Qual é a sua própria área de superfície?

Determine o limite, se existir, ou mostre que o limite não existe.

(Cap. 14.2 – Ex. 13) Determine o limite, se existir, ou mostre que o limite não existe.

(Cap. 14.2 – Ex.26) Determine e o conjunto no qual contínua.

,

(Cap. 14.1 - Ex. 10) Seja

(a) Calcule .

(b) Determine e esboce o domínio de .

(c) Determine a imagem de .

(Cap. 14.1 - Ex. 46) Faça o mapa de contorno da função mostrando várias curvas de nível.

(Cap. 14.2 - Ex. 8) Determine o limite, se existir, ou mostre que o limite não existe.

(Cap. 14.2 - Ex. 12) Determine o limite, se existir, ou mostre que o limite não existe.

(Cap. 14.2 - Ex. 14) Determine o limite, se existir, ou mostre que o limite não existe.

(Cap 14.4 – Ex 2) Encontre uma equação do plano tangente à superfície dado no ponto especificado

(Cap 14.3 – Ex 17) Determine as derivadas parciais de primeira ordem da função.

(Cap 14.4 – Ex 1) Determine a equação do plano tangente à superfície no ponto especificado.

(Cap 14.4 – Ex 6) Determine a equação do plano tangente à superfície no ponto especificado.

(Cap 14.4 – Ex 11) Explique por que a função é diferenciável no ponto dado. A seguir, encontre a linearização da função naquele ponto.

(Cap 14.4 – Ex 42) Suponha que você precise conhecer uma equação do plano tangente a uma superfície S no ponto P (2, 1, 3). Você não tem uma equação para S, mas sabe que as curvas

Ambos estão em S. Encontre uma equação do plano tangente em P

(Cap 14.4 – Ex 34) Use diferenciais para estimar a quantidade de metal em uma lata cilíndrica fechada de de altura e de diâmetro se o metal das tampas de cima e de baixo possui de espessura e o das laterais tem espessura de .

(Cap 14.3 – Ex 80) Se onde mostra isso

(Cap 14.3 – Ex 45) Use a definição de derivadas parciais como limites (4) para encontrar e .

(Capítulo 14.2 – Exercício 38)

Determine o maior conjunto no qual a função é contínua.

(Cap 14.3 – Ex 76) Determine se cada uma das seguintes funções é uma solução da equação de Laplace

(Cap 14.3 – Ex 11) Se , encontre e interprete esses números como inclinações. Ilustre com esboços desenhados à mão ou gráficos de computador.

(Cap 14.4 – Ex 31) Se e varia de a , compare os valores de e .

(Cap 14.4 – Ex 2) Encontre uma equação do plano tangente à superfície dada no ponto especificado

(Capítulo 14.2 – Exercício 37)

Determine o maior conjunto no qual a função é contínua.

(Cap 14.4 – Ex 23) Utilize a tabela do Exemplo 3 para encontrar a aproximação linear da função humidex quando a temperatura está próxima de e a umidade relativa do ar é de aproximadamente . Estime também o humidex quando a temperatura é de e a umidade relativa, .

(Cap 14.4 – Ex 35) Utilize diferenciais para estimar a quantidade de estanho em uma lata cilíndrica fechada com de diâmetro e de altura se a espessura da folha de estanho for de .

(Cap 14.3 – Ex 101e) Seja

(e) O resultado da parte (d) contradiz o Teorema de Clairaut? Use os gráficos de e para ilustrar sua resposta.

(Cap 14.3 – Ex 96c) No estudo de penetração do congelamento descobriu-se que a temperatura no instante (medido em dias) a uma profundidade (medida em pés) pode ser modelada pela função

onde e é uma constante positiva.

(c) Mostre que satisfaz a equação do calor para uma certa constante .

(Cap 14.5 – Ex 3) Use a regra da cadeia para achar .

(Cap 14.3 – Ex 6) Determine os sinais das derivadas parciais da função f cujo gráfico é mostrado

(Cap 14.4 – Ex 41) Um modelo para a área da superfície do corpo humano é dado por , onde é o peso (em quilogramas), é a altura (em centímetros) é medida em centímetros quadrados. Se os erros nas medidas de e forem no máximo de , use diferenciais para estimar a porcentagem de erro máxima na área da superfície calculada.

Seja , onde F, u e v são diferenciáveis, e

Encontre e

(Capítulo 14.6 – Exercício 20) Determine a derivada direcional de em na direção de

(Capítulo 14.6 – Exercício 21) Determine a taxa de variação máxima de no ponto dado e a direção em que isso ocorre.

(Capítulo 14.5 – Exercício 25) Utilize a regra da cadeia para determinar as derivadas parciais indicadas.

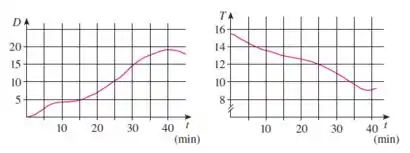
(Capítulo 14.5 – Exercício 37) A velocidade da propagação do som através do oceano com salinidade de 35 partes por milhar foi modelada pela equação

onde C é a velocidade do som (em metros por segundo), T é a temperatura (em graus Celsius) e D é a profundidade abaixo do nível do mar (em metros). Um mergulhador começa um mergulho tranquilo nas águas oceânicas, e a profundidade do mergulho e a temperatura da água ao redor são registradas nos gráficos a seguir. Estime a taxa de variação (em relação ao tempo) da velocidade do som através do oceano experimentada pelo mergulhador 20 minutos depois do início do mergulho. Quais são as unidades?

(Capítulo 14.6 – Exercício 30) Próximo a uma boia, a profundidade de um lago com coordenadas (x,y) é , onde x, y, e z são medidos em metros. Um pescador que está em um pequeno barco parte do ponto (80, 60) em direção à boia, que está localizada no ponto (0, 0). A água sob o barco está ficando mais profunda ou mais rasa quando ele começa a se mover? Explique.

(Capítulo 14.6 – Exercício 34) Suponha que você esteja subindo uma montanha cuja forma é dada pela equação , onde x, y e z são medidos em metros e você está em um ponto com coordenadas (60, 40, 966). O eixo x positivo aponta para o leste e o eixo y positivo aponta para o norte.

(a) Se você andar exatamente para o Sul, começará a subir ou a descer? A que taxa?

(b) Se você caminhar em direção ao Noroeste, começará a subir ou a descer? A que taxa?

(c) Em que direção a inclinação é maior? Qual é a taxa de elevação nessa direção? Qual é o ângulo que o início desse caminho faz em relação à horizontal?

(Capítulo 14.6 – Exercício 42) Encontre uma equação (a) do plano tangente e (b) da reta normal à superfície dada no ponto especificado.

(Capítulo 14.5 – Exercício 40) A voltagem V em um circuito elétrico simples decresce lentamente à medida que a pilha se descarrega. A resistência R aumenta lentamente com o aumento de calor do resistor. Use a Lei de Ohm, , para achar como a corrente I está variando no momento em que , , e

(Capítulo 14.7 – Exercício 10) Determine os valores máximos e mínimos locais e pontos de sela da função.

(Capítulo 14.5 – Exercício 39) O comprimento L, a largura w e a altura h de uma caixa variam com o tempo. Em um determinado momento, as dimensões são e , L e w estão aumentando em uma taxa de 2 m/s enquanto h está decrescendo em uma taxa de 3 m/s. Nesse instante, encontre as taxas em que as seguintes quantidades estão

variando.

(a) O volume

(b) A área da superfície

(c) O comprimento da diagonal

(Capítulo 14.7 – Exercício 49) Determine as dimensões de uma caixa retangular de volume máximo tal que a soma dos comprimentos de suas 12 arestas seja uma constante c.

(Capítulo 14.6 – Exercício 54) Em qual ponto do paraboloide o plano tangente é paralelo ao plano ?

(Capítulo 14.8 – Exercício 8) Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita à(s) restrição(ões) dada(s).

(Capítulo 14.6 – Exercício 31) A temperatura T em uma bola de metal é inversamente proporcional à distância do centro da bola, que tomamos como a origem. A temperatura no ponto (1,2,2) é de 120°.

a) Determine a taxa de variação de T em (1,2,2) em direção ao ponto (2,1,3).

b) Mostre que em qualquer ponto da bola a direção de maior crescimento na temperatura é dada por um vetor que aponta para a origem.

(Capítulo 14.6 – Exercício 11) Determine a derivada direcional da função no ponto dado na direção do vetor .

(Capítulo 14.6 – Exercício 9)

(a) Determine o gradiente de f.

(b) Calcule o gradiente no ponto P.

(c) Determine a taxa de variação de f em P na direção do vetor u.

(Capítulo 14.8 – Exercício 36) Utilize os multiplicadores de Lagrange para dar uma solução alternativa aos exercícios da Seção 14.7 indicados.

Exercício 46

(Capítulo 14.6 – Exercício 32) A temperatura em um ponto (x, y, z) é dada por onde T é medido em ºC e x, y, z em metros.

(a) Determine a taxa de variação da temperatura no ponto P(2, -1, 2) em direção ao ponto (3, -3, 3).

(b) Qual é a direção de maior crescimento da temperatura em P?

(c) Encontre a taxa máxima de crescimento em P.

(Capítulo 14.6 – Exercício 51) Mostre que a equação do plano tangente ao elipsoide no ponto pode ser escrita como

(Capítulo 14.6 – Exercício 24) Determine a taxa de variação máxima de no ponto dado e a direção em que isso ocorre

(Capítulo 14.7 – Exercício 11) Determine os valores máximos e mínimos locais e pontos de sela da função.

(Capítulo 14.7 – Exercício 7) Determine os valores máximos e mínimos locais e pontos de sela da função.

(Capítulo 14.6 – Exercício 4) Determine a derivada direcional de no ponto dado e na direção indicado pelo ângulo .

(Capítulo 14.7 – Exercício 53) Se o comprimento da diagonal de uma caixa retangular deve ser , qual é o maior volume possível?

(Capítulo 14.7 – Exercício 43) Determine três números positivos cuja soma é e cujo o produto é máximo

(Capítulo 14.7 – Exercício 29) Determine os valores máximo e mínimo absolutos de no conjunto .

, é a região triangular fechada com vértices , e .

(Capítulo 14.6 – Exercício 28) Determine as direções em que a derivada direcional de no ponto (0, 2) tem valor 1.

(Capítulo 14.6 – Exercício 12) Determine a derivada direcional da função no ponto dado na direção do vetor .

(Capítulo 14.8 – Exercício 3) Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita à(s) restrição(ões) dada(s).

(Capítulo 14.7 – Exercício 41) Determine os pontos do cone que estão mais próximos do ponto (4, 2, 0).

(Capítulo 14.5 – Exercício 45) Suponha que todas as funções dadas são diferenciáveis.

Se , onde e , (a) determine e e (b) mostre que

Um lado de um triângulo está aumentando a uma taxa de e um segundo lado está decrescendo a uma taxa de . Se a área do triângulo permanece constante, a que taxa varia o ângulo entre os lados quando o primeiro lado tem de comprimento, o segundo lado tem de comprimento e o ângulo é ?

(Capítulo 14.8 – Exercício 31) Utilize os multiplicadores de Lagrange para dar uma solução alternativa aos exercícios da Seção 14.7 indicados.

Exercício 41

Determine os pontos do que estão mais próximos do ponto (4,2,0).

(Capítulo 14.8 – Exercício 28) Use multiplicadores de Lagrange para demonstrar que o triângulo com área máxima, e que tem um perímetro constante p, é equilátero.

(Capítulo 14.8 – Exercício 39) Resolva pelo método dos multiplicadores de Lagrange o exercício da seção .

Determine as dimensões de uma caixa retangular de volume máximo tal que a soma dos comprimentos de suas arestas seja uma constante .

(Capítulo 14.8 – Exercício 9) Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita à(s) restrição(ões) dada(s).

(Capítulo 14.8 – Exercício 4) Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita à(s) restrição(ões) dada(s).