James Stewart – Cálculo Volume 2 – Tradução da 7ª edição americana. Capítulo 15 Seção 4 Problema 22.
(Cap 15.4 – Ex 22) Utilize coordenadas polares para determinar o volume do sólido dado.
Dentro da esfera e fora do cilindro .
Passo 1
Devemos calcular o volume do sólido usando uma integral dupla em coordenadas polares. Como queremos a região fora do cilindro , devemos ter (em polares). Além disso, no plano a interseção da esfera forma o círculo .
Assim, como vamos integrar dentro dela, devemos ter .
Portanto, o domínio de integração será
O cilindro apenas delimita a região de integração, devemos isolar na expressão da esfera para definir que função vamos integrar para achar o volume:
Assim,
Portanto,
Passo 2
Projetando o sólido no plano xy, é um anel e mostrado na figura abaixo
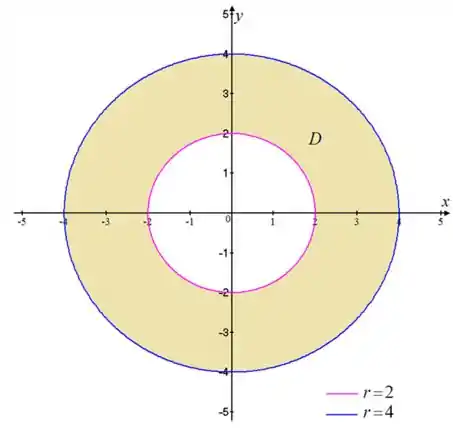
A região sólida é como mostra abaixo
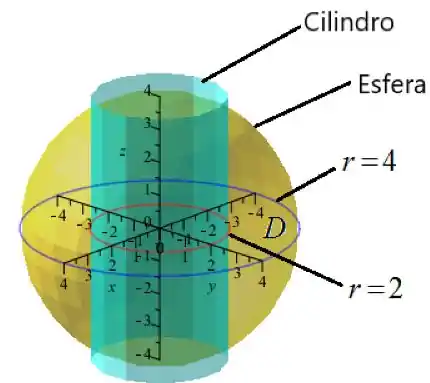
Passo 3
Fazendo a integral em :
Fazendo a mudança , temos que . Assim,
Resposta
Portanto, o volume necessário do sólido é