Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 621234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606163646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

James Stewart – Cálculo Volume 2 – Tradução da 7ª edição americana. Capítulo 15 Seção 4 Problema 17.

(Cap 15.4 – Ex 17) A região dentro do círculo x - 1 2 + y 2 = 1 e fora do círculo x 2 + y 2 = 1 .

Passo 1

Falaiii gurizadaa, baum por dimais da conta?

Simbora pra mais um?

O nosso primeiro passo é visualizar as nossas figuras para podermos compreender como deve ser a região de integração. Para isto, precisamos esboça-los. Portanto,

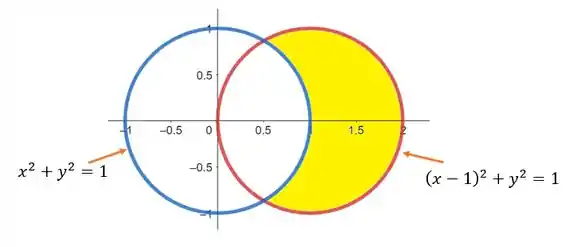
Para podermos esboçar os limites, precisamos passar ambas as curvas para coordenadas polares. A circunferência de centro na origem é expressa por: r = 1 . Agora, vamos desenvolver a outra circunferência. Portanto,

x - 1 2 + y 2 = 1

r cos ⁡ θ - 1 2 + r 2 sen 2 ⁡ θ = 1

r 2 cos 2 ⁡ θ - 2 r cos ⁡ θ + 1 + r 2 sen 2 ⁡ θ = 1 = 1

r 2 - 2 r cos ⁡ θ = 0

r r - 2 cos ⁡ θ = 0

Como r = 0 não é solução, a curva é expressa por r = 2 cos ⁡ θ

Passo 2

Agora que a gente conseguiu compreender a nossa região e obter as curvas me coordenadas polares, podemos determinar os limites da nossa integral dupla. O valor do raio r vai variar da curva mais interna até a curva mais externa. Portanto,

1 ≤ r ≤ 2 cos ⁡ θ

Agora, para determinarmos os valores do ângulo θ , precisamos igualar as duas curvas. Sendo assim, temos:

1 = 2 cos ⁡ θ

cos ⁡ θ = 1 2

θ = π 3   o u - π 3

Portanto, - π 3 ≤ θ ≤ π 3 , o que implica que varia de A até B, pontos destacados no desenho da região. Agora que definimos a região, vamos montar a nossa integral.

∫ - π / 3 π / 3 ∫ 1 2 cos ⁡ θ r d r d θ

Passo 3

Agora, podemos partir para a integração. Portanto,

∫ - π 3 π 3 ∫ 2 cos ⁡ θ 1 r d r d θ

= ∫ - π / 3 π / 3 4 cos 2 ⁡ θ - 1 2 d θ

∫ - π 3 π 3 4 cos 2 ⁡ θ - 1 2 d θ

= ∫ - π / 3 π / 3 2 + 2 cos ⁡ 2 θ - 1 2 d θ

∫ - π 3 π 3 1 + 2 cos ⁡ 2 θ 2 d θ

= θ + sen ⁡ 2 θ 2 - π 3 π 3

π 3 + 3 2 2 - - π 3 - 3 2 2 = π 3 + 3 2

Resposta

Portanto, a área da região R é :

Á r e a = π 3 + 3 2

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}