James Stewart – Cálculo Volume 2 – Tradução da 7ª edição americana. Capítulo 15 Seção 3 Problema 20.
(Cap 15.3 – Ex 20) Calcule a integral dupla.
é limitada por e .
Passo 1
Falaiii gurizadaa, baum por dimais da conta?
Simbora pra mais um?
A região D é delimitada por
Esboçando a região:
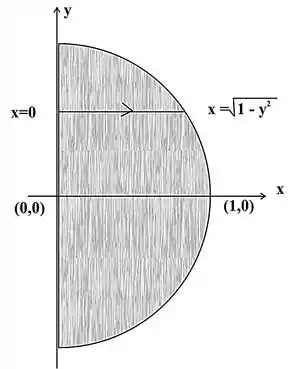
Portanto analisando a região , já podemos deduzir que é uma região do tipo II, já que está representado entre funções de , vamos igualar as equações, se acharmos valores de entre constantes, temos realmente uma região deste tipo.
Elevando ambos os lados ao quadrado
Então temos que
Passo 2
Então temos que
Agora é só integrar, primeiro em relação a
Agora em relação a
Resposta
Exercícios de Livros Relacionados
Determine o volume do sólido dado.Limitado pelos planos x = 0 , y = 0 , z = 0 e x + y + z = 1
Determine o volume do sólido dado.Abaixo do paraboloide z = 3 x 2 + y 2 e acima da região delimitada por y = x e x = y 2 - y .
Calcule as integrais iteradas.int_0^1 int_(x^2)^x ( 1 + 2 y ) d y d x
Calcule a integral dupla. ∬ Dy 2 e x y d A, D = x ,y0 ≤ y ≤ 4,0 ≤ x ≤ y }
Calcule as integrais iteradas. ∫ 0 1 ∫ 0 x 2 ( x + 2 y ) d y d x