Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 701234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697172737475767778798081828384858687888990919293949596979899100

Enunciado

James Stewart – Cálculo Volume 2 – Tradução da 7ª edição americana. Capítulo 15 Seção 4 Problema 8.

(Cap 15.4 – Ex 8) Calcule a integral dada, colocando-a em coordenadas polares.

∬ R 2 x - y d A

Onde R é a região do primeiro quadrante limitada pelo círculo x 2 + y 2 = 4 e as retas x = 0 e y = x .

Passo 1

Falaiiii seres de luz, tudo na paz?

Bora resolver mais uma?

Encostaaaaa

Inicialmente precisamos mudar a função de integração de coordenadas cartesianas para coordenadas polares. Portanto, temos:

∬ R 2 x - y d A = ∬ R 2 r cos ⁡ θ - r sin ⁡ θ d A = ∬ R r 2 2 cos ⁡ θ - sin ⁡ θ d r d θ

Agora, precisamos escrever a nossa região em coordenadas polares. Ela é um retângulo polar. Os limites laterais são dados pelas retas x = 0 , o que implica em θ = π / 2 , e y = x , o que implica em θ = π / 4 . Para obter este último valor, basta fazer:

y = x

r sin ⁡ θ = r cos ⁡ θ

tan ⁡ θ = 1 ⟹ θ = π / 4

Já o raio r varia de 0 até o círculo de raio 2. Logo, 0 ≤ r ≤ 2

Considerando a região R da seguinte maneira, temos

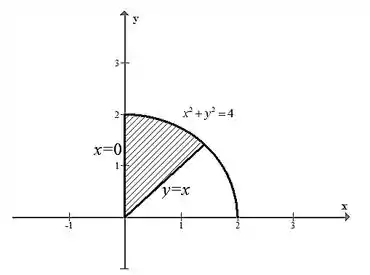
Passo 2

Agora que descrevemos a região em coordenadas polares, podemos colocar os limites de integração na nossa integral. Portanto,

∫ π / 4 π / 2 ∫ 0 2 r 2 2 cos ⁡ θ - sin ⁡ θ d r d θ

∫ π / 4 π / 2 8 3 2 cos ⁡ θ - sin ⁡ θ d θ

= 8 3 ∫ π / 4 π / 2 2 cos ⁡ θ - sen ⁡ θ d θ

= 8 3 2 sin ⁡ θ - - cos ⁡ θ π 4 π 2

= 8 3 2 sin ⁡ θ + cos ⁡ θ π 4 π 2

= 8 3 sin ⁡ π 2 + cos ⁡ π 2 - 2 sin ⁡ π 4 - cos ⁡ π 4

= 8 3 2 1 + 0 - 2 1 2 - 1 2

= 8 3 2 2 - 2 - 1 2

= 8 3 2 2 - 3 2

= 8 3 2 2 2 - 3 2

= 8 3 2 - 3 2

= 16 3 - 8 2  

= 16 3 - 8 2  

= 16 3 - 4 ⋅ 2 2

= 16 3 - 4 ⋅ 2 ⋅ 2 2

= 16 - 4 2

Resposta

Portanto, o valor da integral dada é

∬ R 2 x - y d A = 16 - 4 2

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}