![]()
Passo 1
Vamos começar tentando entender a região de integração. Sem esboçar da pra imaginar que os limites de vão vir dos planos e e que os limites de e vão vir de e .
Então teríamos
E os limites de e vem do esboço no aqui embaixo
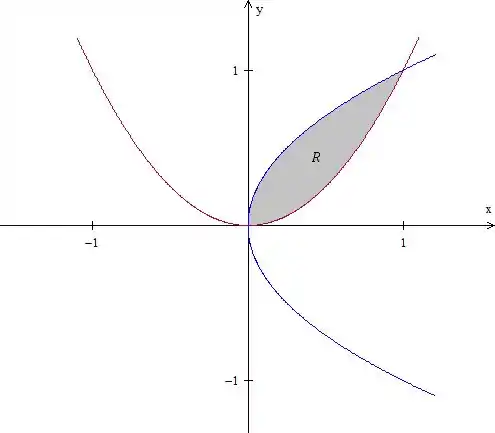
Dando um zoom na região de interesse, podemos fazer a definição tanto pelo quanto pelo , vou fazer aqui pelo primeiro mas dá no mesmo
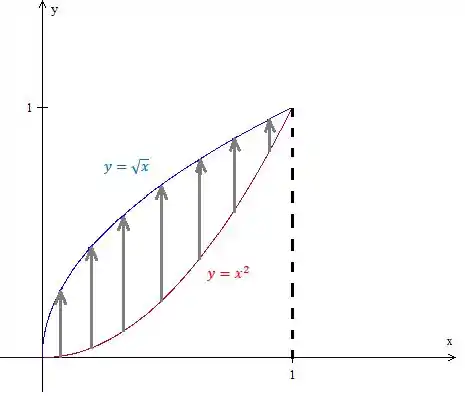
Percebe que a seta sempre entra na curva vermelha e sempre sai em ,tudo isso no intervalo de entre e , logo
Se você quiser saber, o esboço do gráfico é esse aqui, mas percebeu que não precisa dele né?
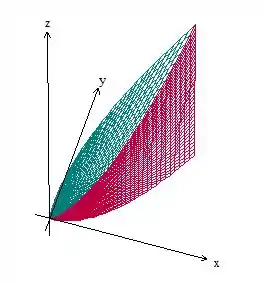
Passo 2
Agora que a gente já definiu a região de integração, é só colocar na integral tripla do enunciado
Passo 3
Integrando em
Integrando em
Essa conta é trabalhosa mesmo, faz com bastante calma tá bem?
Integrando isso aí em
Fazendo o MMC