Calcule a integral tripla
em que é o sólido delimitado pelo cilindro parabólico e e pelos planos e .
Passo 1
Queremos calcular a integral tripla
Onde é a região limitada ao mesmo tempo pelas equações:
A gente precisa descrever essa região usando extremos de integração para poder calcular a integral.
Bora!
Passo 2
Vamos limitar e . Repara que no plano , a projeção da nossa região é a região no plano limitada pelas curvas que dão origem aos cilindros:
é uma parábola virada para cima que passa pela origem, e é uma parábola virada para a direita que também passa pela origem. Repara que nela o termo ao quadrado é o .
Aí esboçando a região limitada por essas curvas
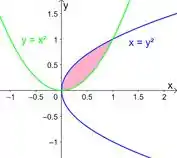
O que a gente precisa fazer aqui é definir essa região como extremos de integração.
Passo 3
Precisamos limitar uma das variáveis entre constantes e a outra pode estar entre funções, beleza?
Vamos começar olhando para o eixo .
A gente pode dizer que nele, a nossa região está limitada entre os valores de e . Essas são as coordenadas das interseções entre e . Podemos ver isso pelo gráfico. Aí dizemos que
Aí olhando para , primeiro a gente precisa isolar em todas as equações para termos , e limitar entre funções de . Aí falta fazer isso com
Agora sim, podemos ver que que nesse eixo, nossa região é limitada por baixo por e por cima por . Aí escrevemos:
Passo 4
Por fim, olhamos a variável . Ele diz que a região está limitada entre e .
Como vimos que nossa região em está no primeiro quadrante, ou seja, , temos que
Aí a gente pode dizer que nossa região é limitada por cima por e por baixo por . Nossos extremos de integração ficam assim:
Passo 5
Agora é montar a integral.
Temos os extremos de integração:
Aí como precisamos integrar primeiro em relação a variável que está entre funções de e , e depois a que está entre funções de , fica assim:
Passo 6
Calculando essa belezura: