UFSC, Araranguá, Cálculo B, P3 - 2022.2, Questão 3
Avalie a integral , onde é o tetraedro com vértices em , e .
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu um tetraedro com vértices em , e e pediu pra gente calcular a integral tripla de nessa região, pra obter o volume.
O primeiro passo pra gente conseguir calcular essa integral é definir os intervalos de integração. Do ponto , a gente sabe que tá variando de a . Pra descobrir como e estão variando, nós vamos precisar analisar o plano e o espaço pra determinar duas funções.
A partir disso, a gente consegue montar a integral na forma:
Então, vamos lá!
Passo 2
Nós já sabemos, pelo passo , que:
Pra descobrir como tá variando, a gente precisa analisar o plano , onde a gente tem os pontos e . Com esses dois pontos, nós conseguimos calcular o coeficiente angular da reta que liga os eixos e no tetraedro.
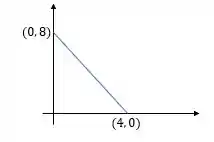
Assim,
Usando a equação geral da reta, nós podemos definir a função :
Substituindo os pontos e o valor de que encontramos, temos:
Passo 3
Agora pra saber como tá variando, nós precisamos olhar para o gráfico do nosso tetraedro:
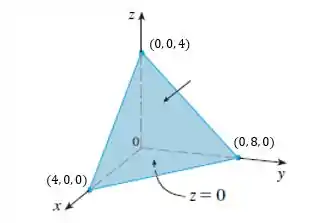
Repare que varia de até uma função no espaço que define aquele plano (face frontal do tetraedro).
Pra definir essa função, nós precisamos definir três vetores linearmente independentes e calcular o determinante deles, que precisa ser igual a zero. Dessa forma, nós podemos definir no espaço os vetores:
E o ponto . Com esses três vetores, calculamos o determinantes na forma:
O resultado vai nos dá uma função , que vai ser nosso terceiro intervalo de integração.
Calculando o determinante, temos:
Dividindo todo mundo por e isolando , temos:
Passo 4
Então, nós já temos nossos intervalos de integração:
E podemos calcular a integral fazendo:
Vamos começar integrando em relação a :
Integrando agora em relação a , temos:
Aplicando os intervalos de integração em :
Por fim, integramos em relação a :
E encontramos nosso volume.
Valeu, galera! 😉