Calcule o volume do sólido limitado pelo cone e o paraboloide .
Passo 1
Bom, o volume desse sólido será , certo? Agora precisamos descrever a região de integração . Vamos começar fazendo um esboço dela:
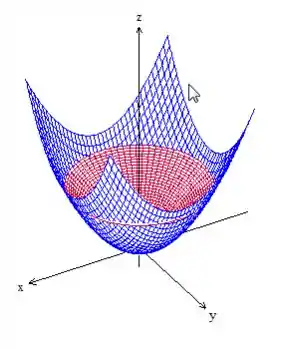
A superfície azul é o paraboloide (virado para cima porque temos e multiplicados por termos positivos), e a vermelha, a folha superior do cone (pois não podemos ter raiz negativa).
Como podemos ver, no plano , temos um domínio . Em , o sólido é limitado embaixo pelo paraboloide e em cima pelo cone . Vamos, então, escrever essa região como tipo I:
Passo 2
Agora precisamos descrever o domínio . Para isso, faremos um esboço da projeção do sólido plano :
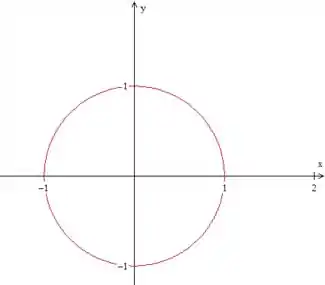
Fazendo a interseção da equação do cone com a equação do paraboloide, temos:
Em as superfícies se encontram, pois ambas partem da origem. Em temos uma circunferência de raio 1. Então, se a projetarmos no plano , teremos a figura acima. Se substituirmos esse valor nas equações das superfícies, encontramos, de fato, .
Como se trata de uma circunferência, vamos escrevê-la com coordenadas polares:
Passo 3
Vamos agora substituir os intervalos que encontramos:
Deixamos para escrever os intervalos de depois para não gerar confusão, pois teremos que fazer a mudança para coordenadas polares.
Passo 4
Integrando em relação a , temos:
Passo 5
Agora vamos descrever a região fazendo a mudança para coordenadas polares (não se esqueça do Jacobiano!). Lembre-se também de que .
Passo 6
Integrando em relação a :
Passo 7
Finamente, integramos em relação a :