Use a integral tripla para determinar o volume do sólido delimitado pelo cilindro e pelos planos e .
Passo 1
Bom, o volume desse sólido será , certo? Agora precisamos descrever a região de integração . Vamos começar fazendo um esboço dela:
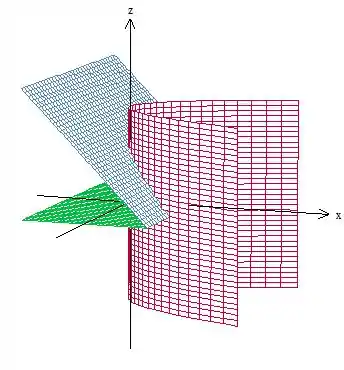
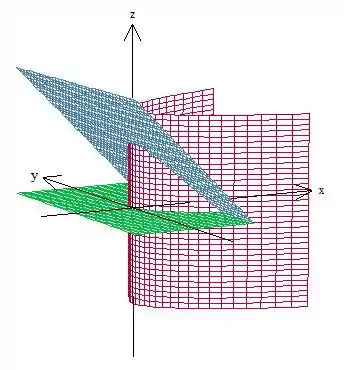
A superfície vermelha representa a equação , que é independente de (ou seja, é a equação de um cilindro), por isso, temos várias parábolas “alinhadas” ao longo desse eixo. O plano azul tem equação independente de , então pode ser interpretado como várias retas ao longo desse eixo.
Como podemos ver, no plano , temos um domínio . Em , o sólido é limitado embaixo pelo plano e em cima pelo outro plano . Vamos, então, escrever essa região como tipo I:
Passo 2
Agora precisamos descrever o domínio . Para isso, faremos um esboço da projeção do sólido plano :
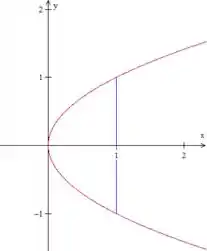
Fazendo a interseção da equação do cilindro e da equação do plano com , descobrimos as equações dessas curvas acima, que serão e .
Vamos descrever essa área como tipo II (poderíamos ter descrito como tipo I também), pois temos o intervalo de entre dois números e o de entre a função da parábola (em vermelho) e a da reta (em azul). Substituindo na equação da parábola, vemos que varia entre e . Temos, então:
Passo 3
Vamos agora substituir os intervalos que encontramos na integral iterada:
Passo 4
Integrando em relação a , temos:
Passo 5
Agora, integramos em relação a :
Passo 6
Finamente, integramos em relação a :