Questão 3: Seja o quadrado no plano limitado pelas retas , , e . No espaço tridimensional, considere a pirâmide sólida com vértice no ponto cuja base é . Calcule a integral tripla da função em .
Passo 1
Primeiramente, o que buscamos resolver aqui mesmo??? Queremos o resultado de uma integral tripla na pirâmide :
Beleza, mas quem é essa pirâmide? Para facilitar a resolução, o que acha de desenha-la comigo? ;)
Passo 2
Veja que a base dela é um quadrado que está entre as retas do problema: , , e ...
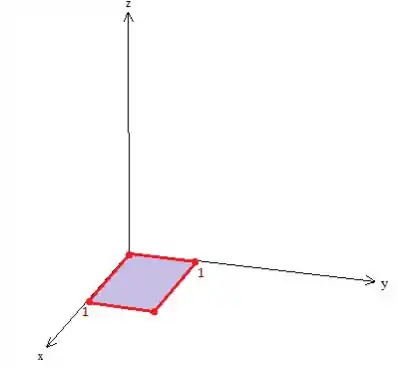
Um quadrado de lado , neh?
Como o vértice da pirâmide está no ponto , a eis que surge a pirâmide...
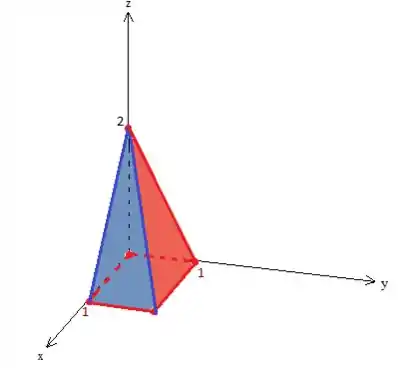
Passo 3
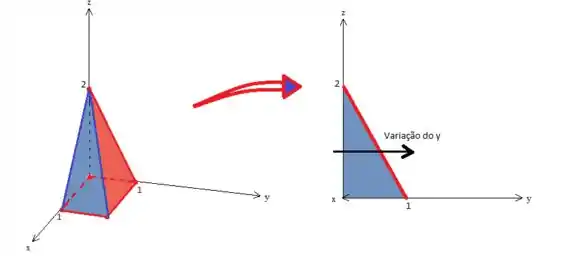
Para resolver uma integral em cima dessa pirâmide, vamos ter que descrever onde variam e dentro dela.
Veja que se a gente visualizar a pirâmide de baixo pra cima, vai varia de até o plano azul de um lado, e do outro ele varia até o plano vermelho. Isso seria um problema pra gente, pois teríamos que editar duas integrais !
Então por esse motivo, é conveniente ver o sólido de ladinho, onde o variam na projeção da pirâmide no plano :
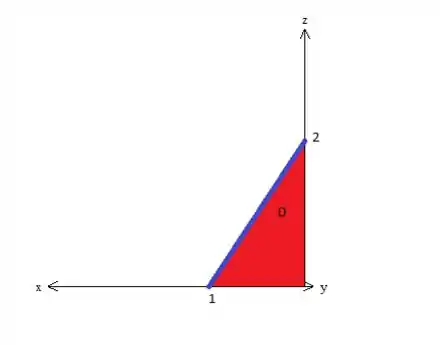
Enquanto que varia de até o plano vermelho, saca?
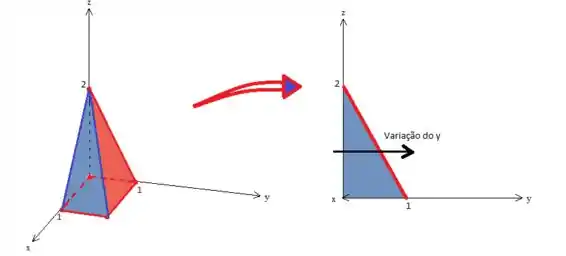
Passo 4
Vamos descrever então aqui a projeção primeiro:
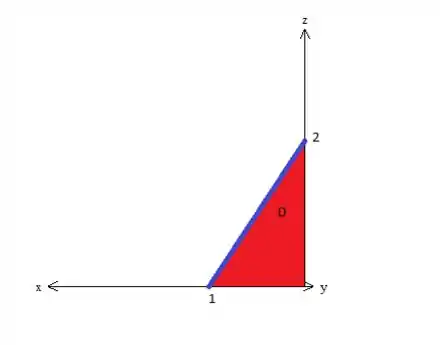
Veja que o varia de até ...
Enquanto que o varia de até a reta azul escuro...
Essa reta aí passa pelo ponto e pelo ponto . Como a equação de uma reta sempre pode ser dado por , basta encontrar e substituindo os pontos...
Então a reta é e a variação de é...
Passo 5
Para descrever então, veja que falar que varia de ao plano vermelho, é o mesmo falar que ele varia de a reta vermelha...
Essa reta vermelha tem equação semelhante a equação da azul de cima, só que no lugar de é o ...
Isolando ...
Logo...
Passo 6
Voltando a integral que queremos resolver...
E trocando os termos de pelas variações...
Bora calcular então?
Passo 7
Calculando a integral de dentro considerando como constante perante a variável de integração...
Agora a do meio...
Chegamos ao valor de...