UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Profº Edson Figueiredo - 2ª Lista, Questão 4
Em coordenadas cartesianas, um ponto P é descrito como . Como este mesmo ponto é representado em coordenadas cilíndricas?
Passo 1
Olá meu amigo, Yuri aqui e agora iremos colocar o nosso ponto dado em coordenadas cilíndricas. No sistema de coordenadas cilíndricas, um ponto P é representado pela tripla ordenada , em que r e θ são as coordenadas polares da projeção de P no plano xy e z é a distância orientada do plano xy ao ponto P.
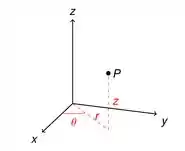
Primeira coisa a fazer é calcular a distancia do ponto a origem, que é dada por
Passo 2
Agora precisamos encontrar o ângulo , ele é dado por
Já o eixo é o mesmo do ponto, então nosso ponto fica como
Resposta
Exercícios de Livros Relacionados
Escrever na forma de uma integral tripla iterada: ∫ ∫ ∫ T f d V Onde T é delimitada por x 2 + z 2 = a 2 ,y 2 + z 2 = a 2
Esboçar a região de integração e calcular as integrais ∫ 0 1 ∫ x 2 x ∫ 0 2 + x + y x d z d y d x
Use a integral tripla para determinar o volume do sólido dado.O sólido delimitado pelo cilindro elíptico 4 x 2 + z 2 = 4 e pelos planos y = 0 e y = z + 2
Calcule a integral iterada. ∫ 0 3 ∫ 0 1 ∫ 0 1 - z 2 z e yd xd zd y
Calcule a integral iterada.int_0^(sqrt(pi)) int_0^x int_0^(x z) x^2 s e n y d y d z d x