Stewart, James. Cálculo, volume 2, ed 7ª – Capítulo 15 – Seção 10 – Questão 22
Passo 1
Fala aí, pessoal! Vamos para um exercício que mostra o cálculo por trás da física do ciclo de Carnot!
Para o exercício em questão teremos que encontrar a melhor substituição para a função de modo a facilitar na hora da integração da função. Para isso vamos manipular as equações e encontrar termos em comum, show de bola?
Vamos começar plotando as funções do ciclo de Carnot que o enunciado nos deu, nós temos isso aqui:
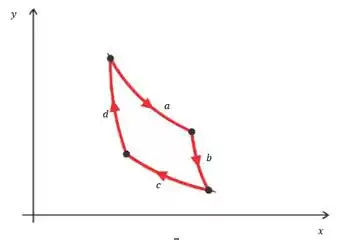
Porém, integrar essas funções exige um trabalho muito maior do que se aplicarmos uma mudança de variável. Podemos separar em dois conjuntos: um deles contendo as isotermas e o outro com as adiabaticas. Temos para o primeiro conjunto as duas equações:
Aplicando a transformação:
E substituindo na equação, ficamos com
Para o segundo conjunto, temos que as equações são:
Aplicando a substituição:
E substituindo na equação, temos que:
Plotando esse novo gráfico ficamos com
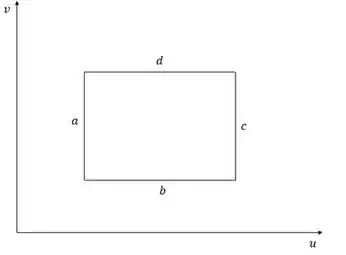
Passo 2
Como foi dito no enunciado, temos que a área do gráfico será o trabalho realizado pelo sistema.
Calculando então a área da segunda figura, temos que:
Integrando nos dois intervalos de integração de e de :
Chegamos a conclusão que o trabalho é igual a:
Bem tranquilinho, concorda comigo? Então te vejo na próxima questão!