Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Triplas em Regiões Gerais

Ver Teoria
Exercício 22123456789101112131415161718192021232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970

Enunciado

(8) O volume do sólido limitado pelas superfícies z = 0 , z = x 2 + y 2 , x = y 2   e x = 2 - y 2 , é dado por:

  1. ∫ - 1 1 ∫ y 2 2 - y 2 ∫ 0 x 2 + y 2 d z d x d y
  2. ∫ - 1 1 ∫ 2 - y 2 y 2 ∫ 0 x 2 + y 2 d z d x d y
  3. ∫ - 1 1 ∫ x 2 - x ∫ 0 x 2 + y 2 d z d x d y
  4. ∫ - 1 1 ∫ 2 - y 2 y 2 ∫ 0 y 4 + y 2 d z d x d y
  5. ∫ - 1 1 ∫ y 2 2 - y 2 ∫ 0 y 4 + y 2 d z d x d y

Passo 1

Bem, o volume para nós a essa altura do campeonato é dado por uma integral tripla, onde calculamos:

V o l u m e = ∭ W   1 d V

O sólido W é o sólido que queremos o volume, no caso precisamos descrevê-lo como sendo de algum tipo. Agora, no nosso caso, quem é o sólido W ?

Passo 2

Ora, basta colocar todas essas superfícies delimitadoras juntas, hehe! :D

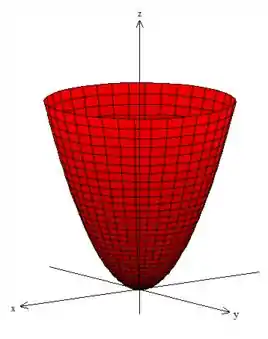
Sabemos que ele está delimitado por esse paraboloide z = x 2 + y 2 ao redor de z :

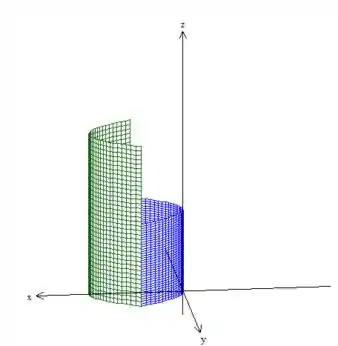
E também por esses dois cilindros parabólicos ao redor de z ... x = y 2 e x = 2 - y 2 (O primeiro representado em azul, e o segundo em verde)

Eis o sólido W em cima do plano z = 0 :

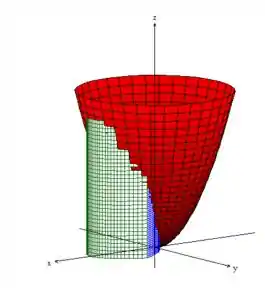
Bem, agora é hora das descrições. Bora?!

Passo 3

Vamos descrever z primeiro.

Repare que o z está variando do plano z = 0 até o topo, o paraboloide vermelho:

0 ≤ z ≤ P a r a b o l ó i d e

Como o paraboloide tem equação z = x 2 + y 2 ...

0 ≤ z ≤ x 2 + y 2

Passo 4

Para a descrição de x e y , olhemos para aprojeção do sólido no plano x y :

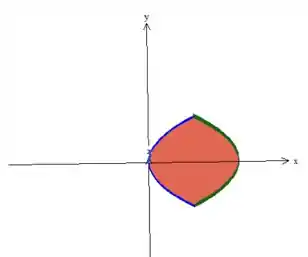
Pow, podemos descrever essa região, como uma do tipo 2 , onde o y varia em um intervalo numérico bem definido!

Para sabermos que variação é essa de y , verifica visualmente que o máximo e o mínimo de y está acontecendo quando esses dois cilindros parabólicos (que no plano são parábolas) se encontram. Eles se encontrarem na matemática é o sistema com suas equações:

x = y 2 x = 2 - y 2           →

y 2 = 2 - y 2     →           2 y 2 = 2           →  

y 2 = 1           →                 y 1 = 1 y 2 = - 1

Logo o y varia de...

- 1 ≤ y ≤ 1

Passo 5

Quanto ao x , veja na mesma projeção que a de cima que o x entra na parábola azul e sai justamente na parábola verde:

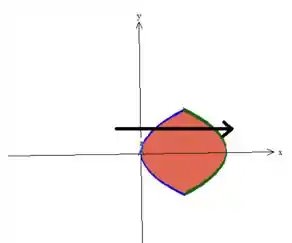
Logo

A z u l ≤ x ≤ V e r d e

y 2 ≤ x ≤ 2 - y 2

Passo 6

Finalmente montando a integral...

V = ∭ W   1 d V

com os dados de variação que temos:

0 ≤ z ≤ x 2 + y 2

y 2 ≤ x ≤ 2 - y 2

- 1 ≤ y ≤ 1

Então:

∫ - 1 1 ∫ y 2 2 - y 2 ∫ 0 x 2 + y 2 d z d x d y

Resposta

a )   ∫ - 1 1 ∫ y 2 2 - y 2 ∫ 0 x 2 + y 2 d z d x d y  

Exercícios de Livros Relacionados

Escrever na forma de uma integral tripla iterada: ∫ ∫ ∫ T f d V Onde T é delimitada por x 2 + z 2 = a 2 ,y 2 + z 2 = a 2
Esboçar a região de integração e calcular as integrais ∫ 0 1 ∫ x 2 x ∫ 0 2 + x + y x d z d y d x
Use a integral tripla para determinar o volume do sólido dado.O sólido delimitado pelo cilindro elíptico 4 x 2 + z 2 = 4 e pelos planos y = 0 e y = z + 2
Calcule a integral iterada. ∫ 0 3 ∫ 0 1 ∫ 0 1 - z 2 z e yd xd zd y
Calcule a integral iterada.int_0^(sqrt(pi)) int_0^x int_0^(x z) x^2 s e n y d y d z d x