Calcule , onde é a região limitada pelo paraboloide e pelo plano .
Passo 1
Vamos fazer um esboço dessa região :
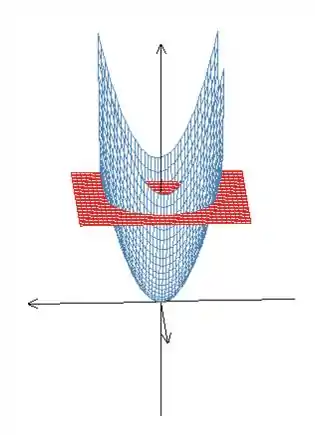
Temos o paraboloide “virado de lado” porque o eixo de simetria é o (o termo que não está elevado ao quadrado).
Como varia entre a equação do paraboloide e e temos, no plano , uma projeção do sólido que representa um domínio (um círculo), vamos descrever essa região como tipo II.
Passo 2
Perceba que o paraboloide é formado por várias circunferências paralelas a , que vão aumentando quando aumenta. A projeção no plano vai ser exatamente a maior dessas circunferências, onde o paraboloide corta o plano . Substituindo esse valor na sua equação, temos então a seguinte circunferência: .
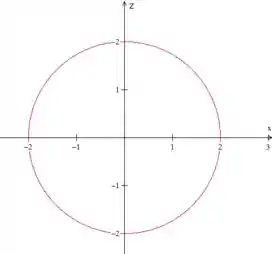
A melhor forma de descrever essa área, como já vimos, é por meio de coordenadas polares, fazendo:
Teremos:
Passo 3
Vamos agora substituir os intervalos que encontramos para a integral iterada. Como tivemos que fazer uma mudança de variáveis para descrever o domínio , vamos escrevê-lo depois da primeira integração, para não gerar confusões. Temos:
Passo 4
Integrando em relação a , temos:
Passo 5
Agora sim, vamos substituir os intervalos de e fazer a substituição polar (Não se esqueça do Jacobiano!).
Você poderia ter feito isso antes, sem problemas. Optamos por fazer assim apenas por questão de organização.
- ''Passo 6
Agora, integramos em relação a :
Passo 7
Finamente, integramos em relação a :