Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Triplas em Regiões Gerais

Ver Teoria
Exercício 66123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646567686970

Enunciado

UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Profº Edson Figueiredo - 2ª Lista, Questão 3

Calcule a integral tripla da função f x , y , z = x 2 z , sobre o sólido limitado pelos planos z = 0 ,   z = 4 e pelo cilindro x 2 + y 2 = 9 .

Passo 1

Olá amigo, Yuri aqui e agora iremos calcula a integral tripla da função que nos foi dada. Lhe convido a primeiro o gráfico da função para que compreendas melhor o que iremos fazer.

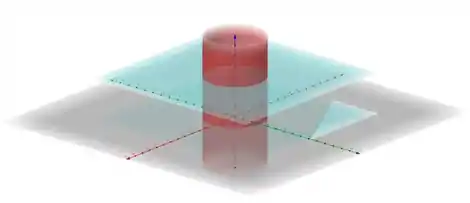
O que temos é, inferiormente e superiormente estamos limitados pelos planos z = 0 e z = 4 , lateralmente estamos sempre limitados pelo cilindro.

Passo 2

Como estamos trabalhando com um cilindro, nada mais justo e interessante o que usar coordenadas cilíndricas para calcular a nossa integral.

x = r cos ⁡ θ

y = r sin ⁡ θ

z = z

Então temos

x = r cos ⁡ θ

y = r sin ⁡ θ

z = z

Com

0 ≤ θ ≤ 2 π

0 ≤ z ≤ 4

0 ≤ r ≤ 3

E com coordenadas cilíndricas nossa função tem a cara de

( r cos ⁡ θ ) ² z

Agora é hora de montarmos nossa integral

∫ 0 2 π ∫ 0 3 ∫ 0 4 ( r cos 2 ⁡ θ ) z r d z d r d θ

Passo 3

∫ 0 2 π ∫ 0 3 ∫ 0 4 ( r cos 2 ⁡ θ ) z r d z d r d θ

8 ∫ 0 2 π ∫ 0 3 r 2 cos 2 ⁡ θ d r d θ

8 ∙ 9 ∫ 0 2 π cos 2 ⁡ θ d θ

Para a integral de ∫ cos 2 ⁡ θ d θ temos primeiro a identidade trigonometria,

∫ 1 + cos ⁡ 2 θ 2 d θ

1 2 ∫ d θ + 1 2 ∫ cos ⁡ 2 θ d θ

1 2 θ + 1 4 sin ⁡ 2 θ

Então agora voltando para a nossa integral tripla após ele leve intervalo

8 ∙ 9 1 2 θ + 1 4 sin ⁡ 2 θ ​ 0 2 π

72 π

Resposta

72 π

Exercícios de Livros Relacionados

Escrever na forma de uma integral tripla iterada: ∫ ∫ ∫ T f d V Onde T é delimitada por x 2 + z 2 = a 2 ,y 2 + z 2 = a 2
Esboçar a região de integração e calcular as integrais ∫ 0 1 ∫ x 2 x ∫ 0 2 + x + y x d z d y d x
Use a integral tripla para determinar o volume do sólido dado.O sólido delimitado pelo cilindro elíptico 4 x 2 + z 2 = 4 e pelos planos y = 0 e y = z + 2
Calcule a integral iterada. ∫ 0 3 ∫ 0 1 ∫ 0 1 - z 2 z e yd xd zd y
Calcule a integral iterada.int_0^(sqrt(pi)) int_0^x int_0^(x z) x^2 s e n y d y d z d x