Calcule as seguintes integrais triplas iteradas:
onde é a região delimitada pelos planos
Passo 1
Bem pessoas, essa é uma questão bem padrão de integração tripla. Ele não deu a integral bonitinha portanto precisamos montar para após isso resolver.
Mas como resolver? Bem, para resolver precisaremos de alguns conceitos de matemática básica e também de conceitos de integração.
Você lembra deles?

CAAAAAAAAAAAAALMA, se lembrar ótimo. Caso contrário vamos resolver aqui passo a passo com você para você aprender certinho belezinha?

Então vaaaaaaaaaaaamos lá
Passo 2
Amigão para resolver um problemão desses precisamos primeiramente montar a região de integração.
Eu sei, eu sei, desenhar essas superfícies 3D é o pipoco do trovão de chato.
Mass nessa aqui a gente não precisa disso tudo, belezinha? Tem um macete.
Geralmente eu tento resolver assim, primeiramente vamos desenhar o domínio da superfície no plano belezinha?
Como faz isso? Bem, fazendo nas equações e vendo o que sobra delas, o só existe naquele plano ali. Então temos a seguinte equação:
Então no plano tua função é algo do tipo:
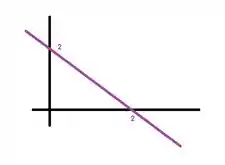
E como a questão diz que está restrita aos planos , então a superfície está no primeiro octante e para finalizar temos que as variáveis estão variando entre:
Logo temos que nossa integral é igual a:
Passo 3
Agora vamos para a parte mais chatinha que é resolver as integrais, eeeeeeeentão vamos lá.
Primeiro resolvendo da integral mais interna:
Utilizando a distributiva, temos que:
Agora integrando o :
Aplicando os limites de integração, temos que:
Realizando as formulas dos quadrados e cubos perfeitos temos que a integral se torna:
Logo temos que a integral vale: