- Use uma integral tripla para calcular o volume do sólido limitado por:
-
, , , .
Passo 1
Cara! Calculo de volume a esse altura do campeonato pra gente é uma integral tripla de :
Não temos uma boa visualização desse sólido por isso sempre é bom começar por aqui
Relaxa, pois fazer isso nada mais é do que desenhar todas essas superfícies aí ao mesmo tempo! Quando fazemos isso, a superfície que ganhamos no espaço é esta daqui, oh:
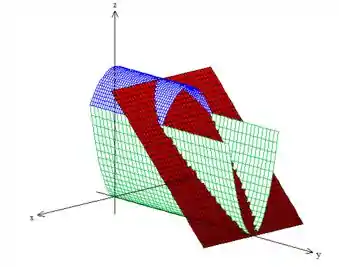
Pegou? :D
Passo 2
Não trabalhamos com esse sólido dessa forma, por isso, a ideia aqui sempre será partir para a descrição dele. Nesse caso, cabe o , onde temos o variando de uma “base” até um “teto”
o plano vermelho é , então isolando o
Quanto ao e ao , olhemos para a projeção do sólido no plano . Bora?
Passo 3
Pow, relaxa! Projetar esse sólido nesse plano nada mais é do que olhar para o sólido
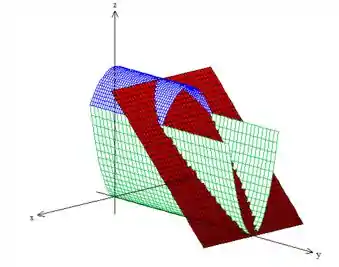
mas dessa vez, colocando o olho em cima do eixo e olhando de ladinho:
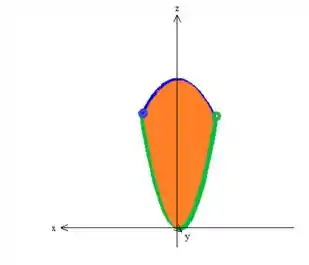
Repare que essas duas curvas verde, , e azul,, são justamente o desenho dessas parábolas no plano . Podemos então descrever a região entre essas parábolas como uma região do , onde
Só nos falta encontrar a variação de e perceba que ele está indo daquele ponto de encontro azul até o verde. Encontrar esses pontos basta resolver a intercessão com as duas parábolas:
Logo
Passo 4
Bem, agora é só montar a integral tripla e correr para o abraço!
Lembre-se que na integral mais interna, fica a que tem mais variável, no caso o , seguido pelo e depois o :
Integrando o de dentro e substituindo os limites de integração
Integrando agora o do meio...
Simplificando esses termos dos parênteses um pouco...
Simplificando mais ainda unindo os termos semelhantes...
chegamos ao resultado, que é