UTFPR, Cornélio Procópio, Cálculo 2, AVF - 2022.2, Questão 5
Encontre o volume da região entre o cilindro e o plano que é delimitado pelos planos , , e .
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu uma região que tá entre um cilindro e um plano , e que é cortado pelos planos , , e . Plotando o gráfico, pra gente entender melhor, ficaria essa coisa bonitinha aqui:
Ocultando os planos, fica mais ou menos isso assim:
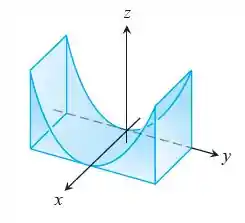
E aí o enunciado pede pra gente calcular o volume dessa região. Mas pra ficar melhor de visualizar, vamos colocar tudo no plano:
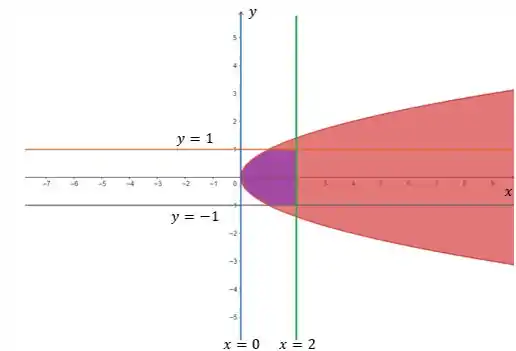
Agora sim, né? Já dá pra ver que a nossa região é essa aí em roxinho. Então, a gente pode usar uma integral tripla pra calcular o volume da região, certo? Ficaria assim:
Então bora calcular essa integral!
Passo 2
Vamos começar integrando em relação a :
Aplicando os limites de :
Integrando agora em relação a , temos:
Aplicando os limites de :
Colocando a constante pra fora da integral:
Integrando agora em relação a :
Aplicando os limites de integração:
E encontramos nosso volume. Até a próxima, galera! 😉