Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Triplas em Regiões Gerais

Ver Teoria
Exercício 39123456789101112131415161718192021222324252627282930313233343536373840414243444546474849505152535455565758596061626364656667686970

Enunciado

UFF, Volta Redonda, Cálculo Diferencial e Integral II, Listas Cálculo Diferencial e Integral II - Lista 2 - Integral Tripla - 2019.1, Questão 1.

1-Calcule a integral tripla ∫ ∫ ∫ W x 2 + y 2 + z 2 d V onde W é a região no espaço (sólido) limitado pelos planos x = 0 , y = 0 , z = 0 e x + y + z = 2 .

Passo 1

Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍

Nesse problema estamos interessados em calcular a integral tripla de x 2 + y 2 + z 2 em W , onde W é limitado pelos planos x = y = z = 0 e x + y + z = 2 .

Tem ideia do que podemos fazer? 🤔

A primeira coisa é visualizar bem a região de integração, depois definir os limites de integração para x , y e z e por fim, calcular a integral...

Parece difícil? Vamos começar! 😁

Passo 2

Os planos x = y = z = 0 nos diz que nossa região está no primeiro octante do espaço.

Já o plano x + y + z = 2 é dado como o plano que corta tanto o eixo x , y e z no ponto 2 , ou seja

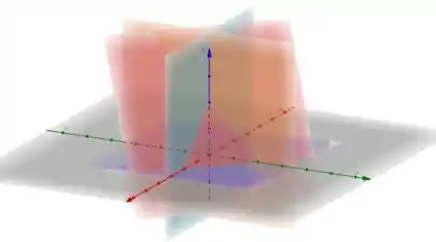
Consegue ver? 👀

O cálculo de uma integral é na verdade o cálculo de um volume, então vamos os limites de x , y e z baseado na equação x + y + z = 2

Assim, podemos definir os limites de integração como 0 ≤ x ≤ 2 - y - z , 0 ≤ y ≤ 2 - z e 0 ≤ z ≤ 2 .

Substituindo na integral, temos

∫ 0 2 ∫ 0 2 - z ∫ 0 2 - y - z x 2 + y 2 + z 2 d x d y d z

Tranquilo até aqui? 😉

Passo 3

Integrando x y z pelo método de integração polinomial, temos

∫ x 2 + y 2 + z 2 d x = x 2 + 1 2 + 1 + x y 2 + x z 2 = x 3 3 + x y 2 + x z 2

Aplicando os limites de integração

∫ 0 2 - y - z x 2 + y 2 + z 2 d x = 2 - y - z 3 3 + 2 - y - z y 2 + 2 - y - z z 2 - 0

∫ 0 2 - y - z x 2 + y 2 + z 2 d x = - 4 y 3 3 - 2 y 2 z + 4 y 2 - 2 y z 2 + 4 y z - 4 y - 4 z 3 3 + 4 z 2 - 4 z + 8 3

Agora integramos o resultado com relação a y

∫ - 4 y 3 3 - 2 y 2 z + 4 y 2 - 2 y z 2 + 4 y z - 4 y - 4 z 3 3 + 4 z 2 - 4 z + 8 3 d y = - 4 y 3 + 1 3 + 1 - 2 y 2 + 1 2 + 1 z + 4 y 2 + 1 2 + 1 - 2 y 1 + 1 1 + 1 z 2 + 4 y 1 + 1 1 + 1 z - 4 y 1 + 1 1 + 1 - 4 z 3 3 y + 4 y z 2 - 4 y z + 8 3 y

∫ - 4 y 3 3 - 2 y 2 z + 4 y 2 - 2 y z 2 + 4 y z - 4 y - 4 z 3 3 + 4 z 2 - 4 z + 8 3 d y = - y 4 - 2 y 3 3 z + 4 y 3 3 - y 2 z 2 + 2 y 2 z - 2 y 2 - 4 z 3 3 y + 4 y z 2 - 4 y z + 8 3 y

Aplicando os limites de integração

∫ 0 2 - z - 4 y 3 3 - 2 y 2 z + 4 y 2 - 2 y z 2 + 4 y z - 4 y - 4 z 3 3 + 4 z 2 - 4 z + 8 3 d y = - 2 - z 4 - 2 2 - z 3 3 z + 4 2 - z 3 3 - 2 - z 2 z 2 + 2 2 - z 2 z - 2 2 - z 2 - 4 z 3 3 2 - z + 4 2 - z z 2 - 4 2 - z z + 8 3 2 - z - 0

∫ 0 2 - z - 4 y 3 3 - 2 y 2 z + 4 y 2 - 2 y z 2 + 4 y z - 4 y - 4 z 3 3 + 4 z 2 - 4 z + 8 3 d y = 2 z 4 3 - 10 z 3 3 + 6 z 2 - 16 z 3 + 8 3

Conta enorme, não é? Mas relaxa, estamos acabando.

Passo 4

Por fim, integramos 2 z 4 3 - 10 z 3 3 + 6 z 2 - 16 z 3 + 8 3 com relação a z

∫ 2 z 4 3 - 10 z 3 3 + 6 z 2 - 16 z 3 + 8 3 d z = 2 z 4 + 1 3 4 + 1 - 10 z 3 + 1 3 3 + 1 + 6 z 2 + 1 2 + 1 - 16 z 1 + 1 3 1 + 1 + 8 3 z

∫ 2 z 4 3 - 10 z 3 3 + 6 z 2 - 16 z 3 + 8 3 d z = 2 z 5 15 - 10 z 4 12 + 2 z 3 - 16 z 2 6 + 8 3 z

Aplicando os limites de integração...

∫ 0 2 2 z 4 3 - 10 z 3 3 + 6 z 2 - 16 z 3 + 8 3 d z = 2 2 5 15 - 10 2 4 12 + 2 2 3 - 16 2 2 6 + 8 3 2 - 0

∫ 0 2 2 z 4 3 - 10 z 3 3 + 6 z 2 - 16 z 3 + 8 3 d z = 8 5

E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí

Resposta

∫ ∫ ∫ W x 2 + y 2 + z 2 d V = 8 5

Exercícios de Livros Relacionados

Escrever na forma de uma integral tripla iterada: ∫ ∫ ∫ T f d V Onde T é delimitada por x 2 + z 2 = a 2 ,y 2 + z 2 = a 2
Esboçar a região de integração e calcular as integrais ∫ 0 1 ∫ x 2 x ∫ 0 2 + x + y x d z d y d x
Use a integral tripla para determinar o volume do sólido dado.O sólido delimitado pelo cilindro elíptico 4 x 2 + z 2 = 4 e pelos planos y = 0 e y = z + 2
Calcule a integral iterada. ∫ 0 3 ∫ 0 1 ∫ 0 1 - z 2 z e yd xd zd y
Calcule a integral iterada.int_0^(sqrt(pi)) int_0^x int_0^(x z) x^2 s e n y d y d z d x