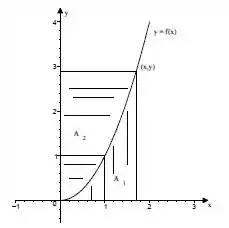
Determine a função cujo gráfico contém o ponto tal que para todo do gráfico de a área da região seja o dobro da área da região , conforme a figura ao lado.
Passo 1
Para começar, temos que:
Pois é a área do retângulo de vértices .
Além disso, o problema diz que:
Substituindo na primeira equação:
Passo 2
OPAAA! Mas quem é ??? Ora, é a integral da função com respeito a .
Mas não sabemos calcular essa integral, certo? Vamos usar o Teorema Fundamental do Cálculo e deriver em ambos os lados com respeito :
E agora a gente resolve essa EDO e descobre quem é .
Separando as variáveis:
Integrando dos dois lados:
Passo 3
Agora vamos usar a informação de que o ponto pertence à curva. Matematicamente, isso quer dizer que:
Resposta
Exercícios de Livros Relacionados
A matrícula em certa universidade vem crescendo a uma taxa de 1000 1 + t - 1 / 2 estudantes por ano desde 1985. Se a matrícula em 1988 foi de 10000:a)qual foi a matrícula em 1985
O volume de um balão está crescendo de acordo com a fórmula d V d t = t + 1 + 2 3 t , onde V em cm³ é o volume do balão em t s. Se V = 33 quando t = 3 , ache:b)O volume do balão em 8 s.
Em cada um dos problemas de 11 a 14, use o método de Euler para encontrar os valores aproximados do problema de valor inicial em t = 0,5 ; 1 ; 1,5 ; 2 ; 2,5e3 .Com h = 0,1 .Com h = 0,05 . Com h = 0,02
Em cada um dos problemas de 11 a 14, use o método de Euler para encontrar os valores aproximados do problema de valor inicial em t = 0,5 ; 1 ; 1,5 ; 2 ; 2,5e3 .Com h = 0,1 .Com h = 0,05 . Com h = 0,02
Uma bola começa a subir em um plano inclinado com uma velocidade inicial de 1,5 m/s. Se há uma aceleração para baixo de 1,2 m/s², até onde a bola subirá no plano antes de começar a descer?