Considere o modelo logístico de dinâmica populacional:
onde , são constantes positivas e .
- Obtenha soluções para o problema de valor inicial ;
- Esboce o gráfico do espaço de fase para o modelo, e determine os pontos de equilíbrio tal que , e classifique estes pontos como estáveis quando ou instáveis quando
Passo 1
a) Para encontrar a nossa solução temos que resolver a EDO, pra isso vamos separar a equação. Dessa forma:
Passo 2
Vamos integrar ambos os lados e resolver cada uma das integrais indefinidas. Resolvendo a equação da esquerda
Vamso utilizar o método das frações parciais, assim:
Temos:
Passo 3
Resolvendo o lado direito da igualdade temos.
Igualando as duas integrais que calculamos.
Essa constante que a gente adiciounou foi justamente pelas constantes das integrais indefinidas que nós não colocamos lá atrás.
Tomando a constante de integração como positiva se e negativa se :
Do PVI temos:
Assim, podemos escrever:
Passo 4
b)Esboçando o gráfico temos:
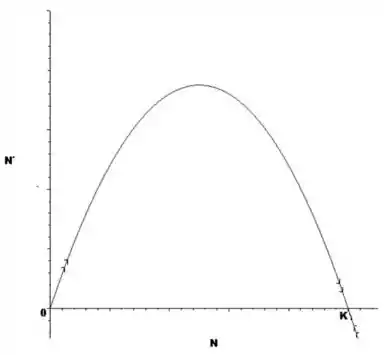
Vemos portanto que, nas proximidades de , tende a se afastar e portanto este é
um ponto de equilíbrio instável, e que, nas proximidades de , tende a se
aproximar (de ambos os lados), e portanto este é um ponto de equilíbrio estável.
Resposta
a)