Uma tigela de sopa sai do aparelho de micro-ondas a e é levada para uma sala onde a temperatura é de . A lei de resfriamento de Newton afirma que a taxa de resfriamento é proporcional à diferença de temperatura entre o objeto e sua vizinhança. Sabemos também que esta sopa esfria a uma taxa de por minuto quando sua temperatura é de :
Escreva a equação diferencial que expressa a lei de resfriamento de Newton nesta situação particular.
Resolva a equação diferencial e determine a temperatura da sopa meia hora após ter chegado à sala.
Esboce um gráfico que represente a temperatura da sopa a partir do momento que chegou a sala.
Passo 1
a)
Vamos com calma, você não precisa saber a lei de resfriamento de Newton. Isso é Cálculo, repara que ele explicou direitinho como é essa lei né? Vamos entender bem essa parada.
Primeiro vamos fazer sendo a temperatura em . Esse vai ser o tempo, repara que no enunciado ele depois da uma taxa em por minuto, assim vamos fazer em minutos para facilitar nossa vida.
Ele disse que a lei de resfriamento de Newton diz que a taxa de resfriamento é proporcional à diferença de temperatura entre o objeto e sua vizinhança. Taxa de resfriamento que dizer a taxa que varia a temperatura, ou seja, a derivada de . Depois ele fala que ela é proporcional a diferença de temperatura entre o objeto e a sua vizinhança. Isso quer dizer que
Quando ele diz que é proporcional a diferença quer dizer que ele é a diferença vezes uma constante, que nesse caso chamamos de .
No enunciado ele diz que a temperatura na vizinhança vai ser
Então vamos ter a seguinte EDO para achar
Passo 2
Você pode olhar e achar que está certinha essa EDO né? Mas temos um ali. Precisamos achar o seu valor. Repara que ele diz no enunciado que
“esta sopa esfria a uma taxa de por minuto quando sua temperatura é de :”
Isso nos diz que
A taxa vai ser porque a temperatura está diminuindo. Então
A nossa EDO vai ser
Passo 3
b)
Repara que do lado direito temos uma função de , isso nos dá uma evidência que essa EDO é separável, vamos trocar por
Agora temos que multiplicar cruzado, deixando tudo que tem na esquerda e tudo que tem na direita. Vamos ter
Agora temos que integrar os dois lados
Resolvendo as integrais vamos ter
Vamos isolar agora
Podemos fazer
E ter
Para tirar aquele módulo vamos ter
Por mais estranho que pareça, podemos fazer
Isso porque aquilo nada mais é que uma constante, como vamos ter uma solução só vamos acabar achando a mesma solução neste caso
A solução geral vai ser
Passo 4
Falta achar o valor de né? Repara que ele deu a temperatura inicial dessa parada, ou seja,
Vamos substituir isso na equação que achamos
A nossa Equação vai ficar
Passo 5
Vamos agora achar o valor da temperatura depois de meia hora, ou seja,
Aqui não tem muito o que fazer não, vamos deixar assim
Passo 6
c)
A nossa função vai ser
Ele agora quer o gráfico dessa parada.
Repara que isso é uma função exponencial, a função exponencial normalmente tem o seguinte gráfico
Isso se tivéssemos , mas na verdade temos aquele expoente negativo, isso vai fazer a função ficar ao contrário. Além disso, a função vai começar em , falta descobrir para qual valor ela se aproxima quando
Vamos fazer esse limite
Então vamos ter
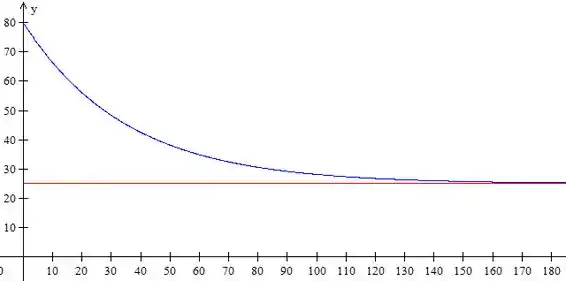
Aquela reta vermelha é , que é a assíntota dessa função.
Resposta
a)
b)
c)
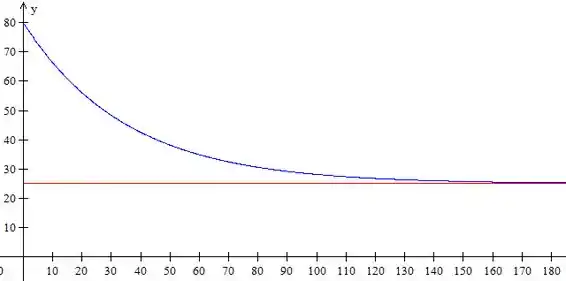
Aquela reta vermelha é , que é a assíntota dessa função.