Um carro está fazendo uma curva apoiado em um plano inclinado da forma indicada na figura ao lado, que mostra o plano transversal ao movimento do carro.
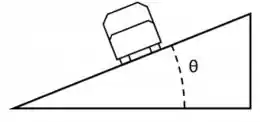
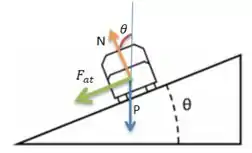
- Faça um esboço das forças que atuam no carro no plano transversal ao movimento. Considere que o atrito é desprezível.
- Desprezando o atrito, encontre a velocidade com a qual o carro está fazendo a curva em função da aceleração da gravidade , do raio de curvatura desta curva, , e do ângulo de inclinação da curva, .
- Deste item em diante, considere agora uma situação em que há atrito e o motorista está correndo na velocidade máxima sem escorregar para fora da curva. Esboce as forças envolvidas no plano transversal nesta situação.
- Encontre a velocidade máxima na qual o carro ainda é capaz de fazer a curva sem derrapar em função de , , e o coeficiente de atrito estático .
Passo 1
POW! Para vamos desenhar as forças aí, temos que antes nos fazer a seguinte pergunta: quem são as forças que atuam nesse carro?
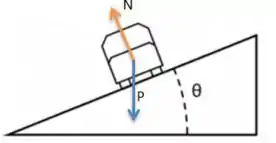
- A primeira força que atua aí é o peso do carro direcionado para baixo:
- A segunda força que atua é a normal direcionada na direção perpendicular do chão porque é justamente a força de reação ao peso feita pelo chão no carro:
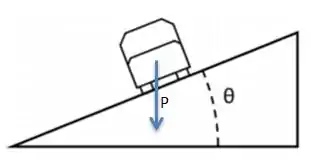
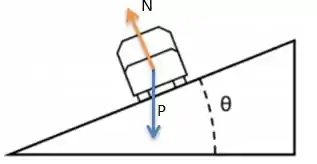
E prontinho! Não tem nenhuma outra força atuando na seção!
Passo 2
Pow! Veja bem, repare que a força normal tem uma leve inclinação para a esquerda. Essa componente que vou chamar de . E como o carro está numa curva, essa força atua como uma força centrípeta !
Bem, de um lado, podemos falar que por trigonometria...
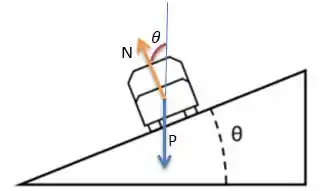
Então...
E de outro lado, a força centrípeta...
Então...
Passo 3
Bem, mas ainda falta a gente falar quem é o .
Pow! Sabemos que a normal está relacionada com o peso, já que não existe movimento na direção normal do plano...
E o peso é então...
Passo 4
Bem, a diferença desses para o outro item é de que temos a força de atrito na parada. O atrito no caso tem que estar para baixo, já que o carro tende a sair da pista...
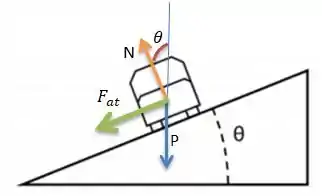
Passo 5
De modo análogo ao anterior, podemos falar que a força centrípeta é a componente . Só que agora tem um diferencial! Além da componente temos também a participação da componente ...
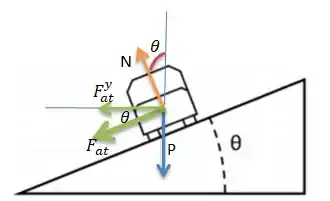
Então...
Só que a força de atrito é a normal vezez o coeficiente de atrito , de modo que...
Passo 6
POW! Então está faltando a gente encontrar quem é a normal .
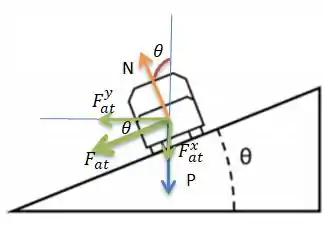
Repare que rebatendo as forças para o eixo ...
Isolando o ...
Concluímos então que a velocidade nessa condição é...
Resposta
Letra A:
Letra B:
Letra C:
Letra D: