Sobre um corpo, de massa , atuam três forças, , e . Duas delas, mostradas na figura abaixo à esquerda, tem módulos iguais a , mas atuam em direções diferentes. O corpo está inicialmente em repouso sobre uma mesa horizontal sem atrito. Na figura da direita, é mostrado um gráfico da velocidade escalar do corpo em função do tempo, onde cada quadrado na vertical equivale a . Considere e .
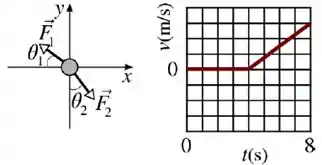
No intervalo entre e sabe-se que o copo se desloca em uma trajetória retilínea no sentido positivo do eixo . Neste intervalo de tempo a força é dada por:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Passo 1
Entre os instantes e , a gente consegue ver no gráfico que a partícula começa a se mover com uma certa aceleração.
Inclusive conseguimos calcular essa aceleração, pois:
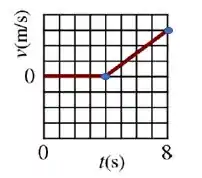
Como cada quadradinho na vertical é igual a , temos que:
Além disso, conseguimos aplicar a Segunda Lei de Newton para encontrar a força resultante agindo sobre a partícula, pois sabemos que a massa é :
O enunciado não disse que a partícula se movimenta na direção positiva do eixo ?
Isso significa que a força resultante sobre o corpo deve estar nessa direção, então:
Passo 2
Essa força resultante será a soma vetorial das três forças atuando sobre o corpo:
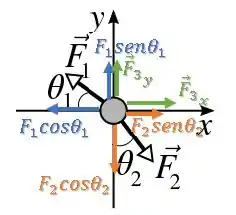
Conhecemos tanto a , quanto a , assim conseguimos encontrar a .
Então, vamos decompor essas duas forças que conhecemos para somar as componentes nos eixos e .
Passo 3
Decompondo primeiro , temos:
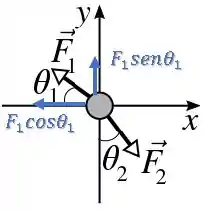
Decompondo agora , temos:
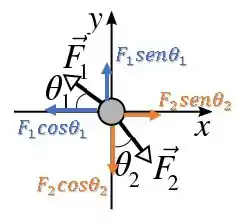
Além disso, existe também a que até agora é desconhecida, então vamos considerar uma componente em e uma em nos sentidos positivos. Mas, depois de realizar as contas vamos saber realmente o sentido dessas componentes:
Passo 4
Agora, vamos somar todas essas componentes para achar a força resultante e igualar com o valor que encontramos no Passo 1.
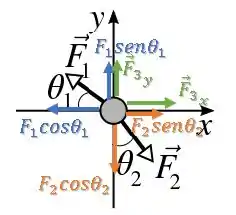
Na direção do eixo , temos que a força resultante é igual a :
Substituindo os valores que temos no enunciado de , e os senos e cossenos:
Enquanto no eixo , a força resultante é nula:
Juntando as duas componentes de , ficamos com o vetor:
Ficamos com a letra (g).
Resposta
Letra g.