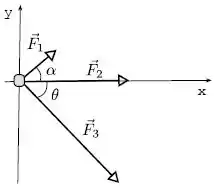
Uma partícula de massa encontra-se sob a ação de três forças constantes, como mostra a figura abaixo. Os módulos das forças são , e . Os ângulos da figura são tais que , , e . Determine o vetor aceleração da partícula.
Passo 1
Temos uma partícula e três forças aplicadas sobre ela.
Mas cada uma aponta em uma direção diferente, então vamos fazer o somatório vetorial delas e depois achar a aceleração através da segunda lei de Newton:
Passo 2
Vamos decompor cada uma dessas forças nos eixos e .
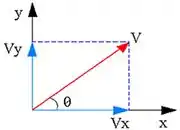
Como e são os ângulos medidos a partir do eixo , nos dois caso, temos que as componentes horizontais e verticais serão:
Vamos começar com :
Para , como a força está na horizontal, sua componente em é ela mesma:
Já , temos que:
Porém, ela aponta para baixo. Logo, sua componente em é negativa:
Passo 3
Vamos fazer o somatório em cada eixo agora.
No eixo :
No eixo :
Então, temos que a força resultante é:
Passo 4
Agora, basta calcularmos o vetor aceleração com:
A massa é :