UFABC – Fenômenos Mecânicos – Lista 3 – Questão 10
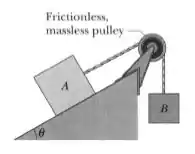
Na figura abaixo dois blocos estão conectados por um fio que passa por uma polia. A massa do bloco é e o coeficiente de atrito cinético entre e a rampa é . O ângulo da rampa é . O bloco desliza para baixo ao longo da rampa com velocidade constante. Qual é a massa do bloco ?
Passo 1
Oi pessoal, tudo bem? Esse sistema se movimenta com velocidade constante, isso significa que as forças estão em equilíbrio
Para determinar a massa do bloco B é preciso equacionar as forças do sistema e verificar qual é a condição para termos essa situação de igualdade de forças mas relaxa, vou fazer passo a passo com você!
Belezera galera, se a gente desenhar as forças que atuam no sistema, vamos obter um desenho mais ou menos assim:
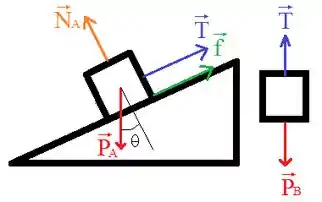
O sistema desliza pra baixo, então a força de atrito é voltado rampa acima (vetor em verde). As tensões são iguais, e estão representadas m azul. Temos a força de sustentação do bloco A no plano e os pesos dos blocos, verticalmente para baixo.
a normal equilibra a componente vertical do peso A, e a tensão e a força de atrito (no bloco A) são equilibradas pela componente horizontal do peso A.
no próximo passo vamos equacionar as forças!
Passo 2
Vamos começar analisando o bloco , lembrando que, como os blocos se movimentam com velocidade constante, a aceleração é nula. Assim, para cada eixo temos:
Lembrando que a força de atrito cinética pode ser definida por:
Tranquilo?
Passo 3
Aplicando agora a segunda lei de Newton para o bloco :
Inicialmente vamos determinar o valor da força de atrito. Para isso, vamos isolar a normal na :
Mas , aí:
Beleza?
Passo 4
Agora vamos resgatar as equações a e isolar :
Daí a tensão fica:
Certo? Agora vamos resgatar a equação (4) do passo anterior
Substituindo a na :
Isolando , dividindo tudo por e substituindo os valores conhecidos:
E é isso! Espero ter ajudado!