Universidade Federal do Rio de Janeiro- P1-2020.02
Questão 10
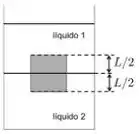
É constatado que um determinado corpo homogêneo de forma cúbica está em equilíbrio quando imerso em uma mistura de dois líquidos imiscíveis de modo que metade está imersa no líquido 1 e outra metade está no líquido 2, como na figura. Quando este mesmo corpo é colocado em um recipiente somente com líquido 2, é correto afirmar que:
Passo 1
Fala galerinha tranquilidade, essa questão é bastante interessante, está relacionando o empuxo em dois líquidos, temos que estar bastante atentos ao fato que o empuxo é sempre para cima, significando que se são dois empuxos vamos somar. Primeiro vou desenhar o esquema da situação um que é dada pelo problema.
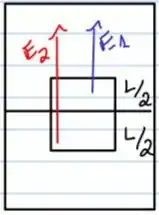
Agora vamos equacionar cada um dos empuxos, o primeiro temos:
A soma dos volumes é porque ele desloca com o seu volume total.
Para a parte vermelha do empuxo que é o empuxo 2 temos;
Passo 2
Passo 3
Passo 4
Como dissemos anteriormente o empuxo é sempre para cima, com isso temos a soma dos empuxos, para o empuxo resultante da situação 1
Abrindo os cálculos do empuxo da situação 1 ficamos:
Podemos eliminar os termos que são iguais ficando:
Como sabemos que é um cubo de aresta L e que só metade está imersa em cada um dos líquidos podemos colocar:
Passo 5
Agora que sabemos o comportamento do empuxo em dois líquidos vamos comparar a segunda situação onde temos a atuação apenas do líquido 2.
Resposta
Agora podemos relacionar os empuxos considerando os fatores que serão considerados.
>, esse resultado indica que o volume deslocado no líquido 2 é menor, e isso faz todo sentido considerando que ele tem uma densidade maior que o líquido 1.