Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Segunda Lei de Newton

Ver Teoria
Exercício 351234567891011121314151617181920212223242526272829303132333436373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Enunciado das questões (Q6) e (Q7).

Um cilindro uniforme de massa m 1 e raio R está apoiado num eixo horizontal, podendo girar livremente, sem atrito. Uma corda enrolada no cilindro prende um bloco de massa m 2 , que pode deslizar sem atrito sobre um plano inclinado de ângulo θ , como mostra a figura. O sistema é solto, a partir do repouso, quando m 2 está a uma altura h acima da horizontal.

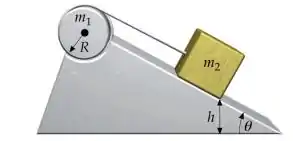
(Q6) [1,0 ponto] Considerando que a corda não desliza sobre o cilindro, a aceleração de m 2 é:

  1. a = m 1 + 2 m 2 g sin ⁡ θ m 1 + m 2
  2. a = 2 m 2   g sin ⁡ θ m 1 + 2 m 2
  3. a = m 2   g sin ⁡ θ m 1 + 2 m 2
  4. a = m 1   g sin ⁡ θ 2 m 1 + m 2
  5. a = 2 m 1   g sin ⁡ θ m 1 + 2 m 2

Passo 1

POW! Sabemos que a aceleração a do bloco tem tudo haver com a segunda Lei de Newton, ou seja...

F t o t = m 2 a     →

a = F t o t m 2

Onde F t o t é a força total na direção do movimento (tangencial do plano).

Então veja que basta saber quem é a força total e o nosso problema estará resolvido . Vamos nessa?

Passo 2

Para encontrar essa força total, podemos desenhar o diagrama de forças livres...

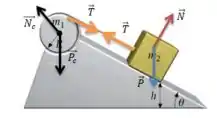
Olhando apenas para o bloco agora, o a normal ta ali só porque ela existe devido ao contato com o chão, mas ela não se intromete no deslocamento do bloco, portanto você pode esquecê-la por enquanto, ta bom? As duas únicas forças que vão influenciar no deslocamento do bloco serão a tração T → e a componente tangencial do peso P t → ...

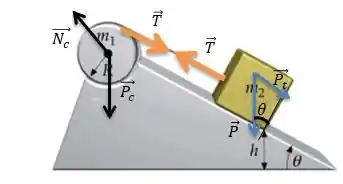
Por trigonometria...

P t = P sin ⁡ θ

Então, a força total na direção tangencial que vai fazer o bloco deslizar na rampa será...

F t o t = P t - T = m 2 g sin ⁡ θ - T

Logo...

a = m 2 g sin ⁡ θ - T m 2

Tá, mas quem é a tração T ?

Passo 3

Bem, é aqui que entra a informação do cilindro .

Sabemos que quando o bloco começar a descer, o cilindro vai começar a girar. Se ele vai começar a girar, então podemos falar que para um ponto na borda, veremos uma aceleração angular α de modo que...

α = τ I

Onde I é o momento de inércia do cilindro que vale I = 1 2 m 1 R 2 ...

α = τ 1 2 m 1 R 2

O torque τ que faz o cilindro girar é causado pela força T (força que é tangencial ao cilindro). Esse torque então será...

τ = T R

Logo...

α = T R 1 2 m 1 R 2       →

α = 2 T m 1 R       →

Ta, mas o que a aceleração angular do cilindro tem haver com a aceleração do a do bloco?

Passo 4

Bem... A aceleração a do bloco também vai ser a aceleração tangencial do cilindro que se relaciona com a aceleração angular por...

α = a R

Então...

a R = 2 T m 1 R       →

T = m 1 2 a

Passo 5

SHOW de bolinhas . Agora é só a gente pegar esse resultado e voltar para a equação que encontramos no passo 2...

a = m 2 g sin ⁡ θ - T m 2     →

a = m 2 g sin ⁡ θ - m 1 2 a m 2       →

Agora é só partir para a simplificação!

a = m 2 g sin ⁡ θ m 2 - m 1 2 m 2 a       →

Passando para o outro lado...

a + m 1 2 m 2 a   = g sin ⁡ θ →

a 1 + m 1 2 m 2   = g sin ⁡ θ →

Passando dividindo...

a   = g sin ⁡ θ 1 + m 1 2 m 2 →

Multiplicando e dividindo por 2 m 2 ...

a   = 2 m 2 g sin ⁡ θ 2 m 2 + m 1

Resposta

Letra B

Exercícios de Livros Relacionados

Existem duas forças horizontais atuando na caixa de 2,00k g da Fig. 5-39, mas a vista superior mostra apenas uma (de módulo F 1 = 20N ). A caixa se move ao longo do eixo x . Para cada um dos valores d
Propulsão solar. Um "iate solar'' é uma nave espacial com uma grande vela que é empurrada pela luz do Sol. Embora esse empurrão seja fraco em circunstâncias normais, pode ser suficiente para afastar a
Uma força horizontal constante F → a empurra um pacote dos correios de 2,00k g sobre um piso sem atrito onde um sistema de coordenadasx y foi desenhado. A Fig. 5-37 mostra as componentes x e y da velo
Você puxa um pequeno refrigerador com uma força constante em um piso encerado (sem atrito), com na horizontal (caso 1) ou com inclinada para cima de um ângulo θ (caso 2). (a) Qual é a razão entre a ve
Duas forças horizontais agem sobre um bloco de madeira de 2,0k g que pode deslizar sem atrito em uma bancada de cozinha, situada em um plano x y . Uma das forças éF → 1 =3,0N i →+4,0N j → . Determine