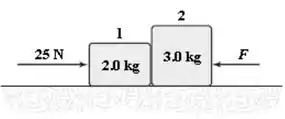
8) Considere a situação mostrada na figura ao lado. Não há atrito entre os blocos e a superfície horizontal. Se , qual é o módulo da força Exercida pelo bloco 2 sobre o bloco 1?
a)
b)
c)
d)
e)
Passo 1
Fala aí, galerinha! Tudo belezinha com vocês?
Bom, a questão deu pra gente a imagem desse sistema de dois blocos e disse que uma força está agindo sobre o bloco 2, e pediu pra gente calcular a força que o bloco 2 exerce no bloco 1.
Bom, pra gente começar a fazer essa questão, precisamos lembrar da terceira lei de Newton que diz que:
“A toda ação corresponde a uma reação de igual intensidade, mas que atua no sentido oposto”
Isso quer dizer que a força que o bloco 1 faz no bloco 2 é igual a força que o bloco 2 faz no bloco 1. E analisando o diagrama do corpo livre para cada um dos blocos, poderemos descobrir o valor dessas forças.
Então esse é o plano. Vamos fazer o diagrama do corpo livre para cada um dos blocos e ver o que conseguimos encontrar para resolver nosso problema.
Partiu!!!
Passo 2
Vamos começar fazendo o diagrama para o corpo 1. Perceba que no eixo as forças Peso e Normal irão se cancelar, então só faremos o diagrama pra o eixo onde pode acontecer o movimento do sistema. Assim:
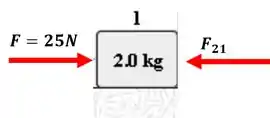
Aplicando a segunda lei de Newton para esse bloco ficamos com:
Substituindo o que conhecemos, ficamos com:
Maravilha. Vamos dar uma olhada agora no bloco 2:
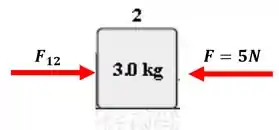
Da mesma forma que fizemos com o bloco 1, podemos aplicar a segunda lei de Newton para esse bloco ficamos com:
Substituindo o que conhecemos, ficamos com:
E com essas duas equações, podemos montar um sistema que nos ajudará a conhecer a aceleração dos blocos, e depois poderemos usar uma delas para calcular a força que estamos procurando. Veremos isso no próximo passo.
Passo 3
Até agora vimos que:
E
O que nos dá o sistema:
Como , podemos somar as duas equações, ficando com:
Pronto! Agora que temos a aceleração, basta substituir em uma das duas equações que encontramos para obter . Então:
Prontinho! Força encontrada!
Resposta
Resposta: