UFSCAR, Sem Campus, Física 1, Listas Física 1 - UFSCAR - Lista 4 - Rotação, rolamento e corpos rígidos, Questão 6
Um cilindro de massa e raio está rodando sobre uma fenda em com uma velocidade angular . O coeficiente de atrito entre o cilindro e a superfície é .
Qual é o torque externo necessário aplicado no cilindro para que ele se mantenha rotacionando com velocidade constante?
Expresse suas respostas em termos das variáveis do exercício e considere para a aceleração da gravidade.
Passo 1
Fala aí pessoal tudo bom com vocês?
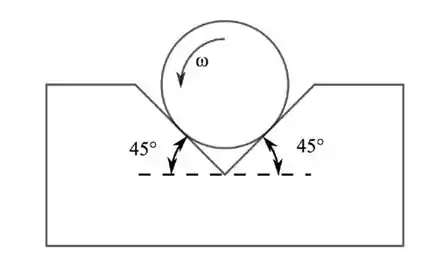
Nessa questão temos um cilindro, conforme mostrado na figura, que está rotacionando sem sair da fenda em . Na superfície da fenda há atrito e também a normal atuando no cilindro.
O enunciado nos pede para calcular qual o torque externo necessário pra que o cilindro permaneça girando com velocidade constante.
Sacaram?!
Pois bem, tem uma equação muito importante envolvendo movimentos de rotação que diz:
Onde é o torque resultante no corpo. Como queremos que a velocidade do corpo seja nula, teremos . Assim:
Ou seja, o que o enunciado realmente nos está pedindo é para calcular o torque externo necessário para que o torque resultante seja nulo.
Pra responder essa pergunta precisamos primeiro avaliar quais as forças que estão atuando no cilindro e calcular o torque com relação ao seu centro. A partir disso, podemos equacionar uma variável para o torque externo, de modo que ele zere o momento resultante.
Tranquilo? Vamo nessa!
Passo 2
Bom, no cilindro estão atuando as seguintes forças:
- Força peso no centro do cilindro;
- Duas reações normais de contato na fenda em ;
- Duas forças de atrito nos dois contatos da fenda em .
Assim, temos o seguinte diagrama de forças para o cilindro:
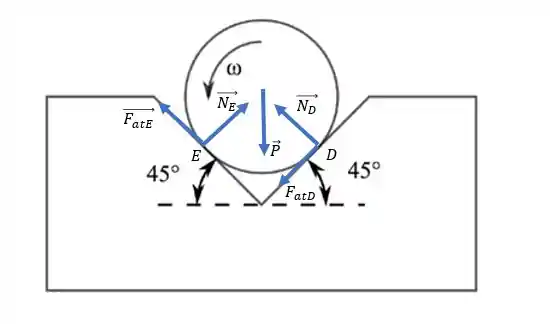
(O sentido da força de atrito leva em conta que o cilindro roda no sentido anti-horário, assim o atrito deve ir contra a tendência desse movimento no ponto de contato).
Como estamos numa situação de equilíbrio estático, pois o cilindro apenas rotaciona, temos que:
Beleza! Muito bom 😊
Passo 3
Agora que já vimos como as forças estão distribuídas, podemos usar as equações do equilíbrio estático. Começando pelo somatório de forças na vertical igual a zero, temos:
Excelente! Tomando agora o equilíbrio de forças na horizontal, temos:
Juntando as duas equações, encontramos que:
Daí:
Muito bom!!
Passo 4
Agora que já sabemos o valor das forças em função dos dados do enunciado, podemos utilizar a equação do momento. Vimos no passo que devemos ter:
Isso considerando o torque externo, que chamaremos de . Assim, tomando o centro do cilindro para calcular os momentos, apenas as forças de atrito e o torque externo exercerão torque. Logo:
Portanto:
Prontinho, galera! Matamos mais uma questãozita!
Vocês curtiram a solução? Responde Aí!