UFSCAR, Sem Campus, Física 1, Listas Física 1 - UFSCAR - Lista 4 - Rotação, rolamento e corpos rígidos, Questão 4
Uma haste uniforme de comprimento e massa está presa num muro por uma de suas extremidades. Na outra extremidade, está amarrado um cabo que é ligado ao muro. O cabo faz um ângulo com a haste. Assuma que o cabo tenha massa desprezível, mas existe forças de contato nele.
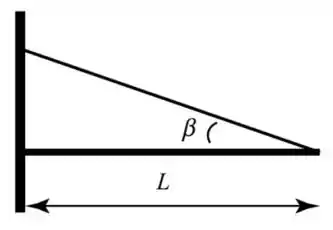
- Qual é a magnitude da tensão no cabo?
- Qual o ângulo da força de contato entre a haste e o muro?
- Qual a magnitude da força de contato entre a haste e o muro?
Passo 1
E aí gente, tudo bom com vocês?
Temos uma questão bem legal envolvendo situações de equilíbrio estático.
Basicamente, temos uma haste na horizontal que está presa a um muro em um dos lados (tipo presa mesmo sabe? parafusada ou algo assim).
Daí, um cabo é conectado na outra extremidade da barra, sendo ele responsável por manter a barra na horizontal, sacaram?
Bom, o objetivo do enunciado é que a gente descubra a tração no cabo, e as forças de contato envolvendo a haste e o muro.
Pra fazer isso, vamos primeiramente fazer o diagrama de corpo livre do nosso sistema. Depois, podemos usar o fato do equilíbrio estático pra usar que:
Beleza?
Então vamo nessa!
Passo 2
Vamos começar pelo DCL. Na haste estão atuando:
- Duas componentes da força de contato da haste com o muro;
- A força peso;
- A Tensão na haste.
Massa! Já no cabo, atuam: a Tensão e a força de contato do cabo com o muro.
Assim, vamos ter o seguinte DCL:
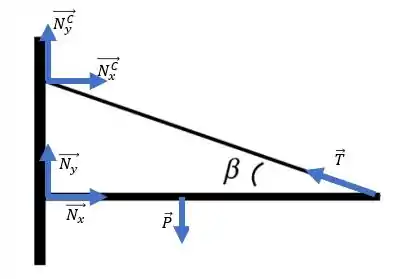
Muito bom!
Passo 3
Agora que já temos o nosso DCL, podemos usar as equações decorrentes do equilíbrio estático. Começando pela somatória de momentos igual a zero. Precisamos escolher o ponto que vamos fazer o momento com bastante sabedoria haha.
Como queremos determinar a tensão no cabo e e , podemos escolher o ponto de contato do cabo com o muro. Assim, já tiramos da nossa equação várias forças cujas linhas de força passam por esse ponto.
Logo, vamos ter que:
Como , e a somatória de momentos é nula. Temos:
Como a massa da haste vale , temos:
Massa! Mas a pergunta inicial é o valor da tensão no cabo, certo?
Pra descobri-la podemos usar que o somatório das forças que atuam na haste na direção horizontal precisa ser . Ou seja:
Perfeito! A primeira pergunta já foi respondida!
Passo 4
A próxima pergunta é sobre qual o ângulo entre a resultante da força de contato da haste com o muro e o próprio muro.
A ideia aqui é pensar no seguinte triângulo:
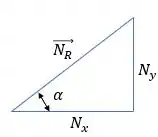
O ângulo que a questão nos pede é justamente . Sacaram?
Pra descobri-lo podemos usar a tangente do triângulo acima, é só descobrir quanto vale e já podemos fazer isso.
Pra descobrir podemos usar que a resultante das forças verticais atuando na haste é nula. Assim:
Como :
Logo:
Massa! Portanto:
Logo, temos que . Assim, o ângulo pedido vale:
Excelente galera!!
Passo 5
A última pergunta é sobre qual o valor da resultante de contato entre a haste e o muro. Ou seja, quanto que vale .
Basta fazermos:
É isso então galera! Muito obrigado pela atenção de vocês e até a próxima 😊