Um plano inclinado de massa M repousa em uma mesa horizontal sem atrito. Um bloco de massa m é colocado sobre esse plano (figura abaixo). Não existe atrito entre o bloco e o plano. O sistema é liberado do repouso.
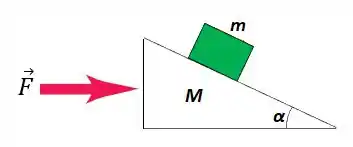
(a) Calcule a aceleração do plano e as componentes horizontal e vertical de aceleração do bloco.
Passo 1
Eaee!!! Belezinha? Olha.. vamos primeiramente fazer um diagrama do corpo livre do bloco e da rampa e aí a gente aplica a 2ª Lei de Newton para podermos entender melhor essa questão, certinho? Se liga:
- Para a rampa:
- Para o bloco:
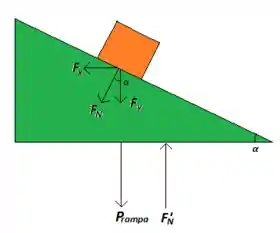
No eixo , temos que:
No eixo , temos:
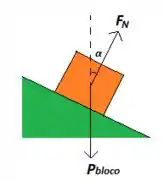
No eixo , temos:
E, no eixo , temos:
Passo 2
Assim, considerando também que os blocos se manterão juntos, temos as seguintes relações entre as acelerações:
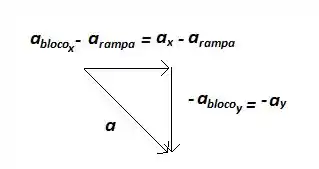
Em que desse triângulo podemos extrair:
Passo 3
Assim, com esses dados, temos as seguintes equações:
Passo 4
Assim, substituindo (3) em (2), temos:
E, substituindo (1) em (3):
Passo 5
Dessa forma, substituindo essas duas equações que encontramos no Passo 4 e simplificando, temos:
Assim, substituindo na expressão de , temos:
E, também substituindo na expressão de , temos:
Entendeu direitinho? Responde aeee!!
