UFSCAR, Sem Campus, Física 1, Listas Física 1 - UFSCAR - Lista 4 - Rotação, rolamento e corpos rígidos, Questão 7
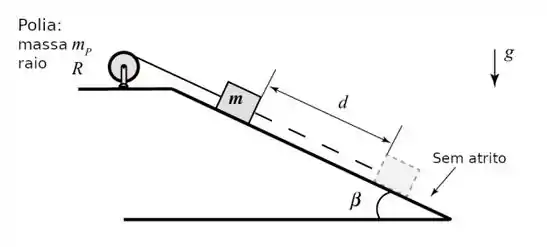
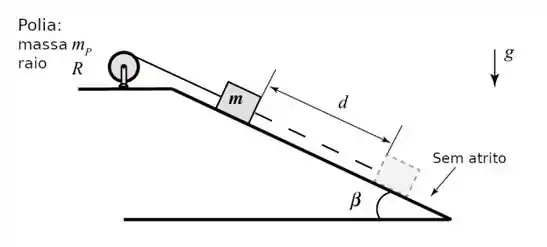
Considere uma polia de massa com raio que tem momento de inércia igual a . A polia é livre para rodar em torno de um eixo central sem atrito. Uma corda sem massa é amarrada por uma extremidade na polia e na outra extremidade é atada a um bloco de massa , que está em repouso sobre um plano inclinado de ângulo com respeito a horizontal. A magnitude da aceleração da gravidade é . Então, permite-se que o bloco deslize. Quanto tempo leva para o bloco andar de uma distância no plano inclinado? Escreva sua resposta usando as variáveis do exercício.
Passo 1
Fala aí pessoal, tudo bem com vocês?
Nessa questão temos um bloquinho em um plano inclinado, que está preso a uma corda que por sua vez passa por uma polia. A massa do bloquinho, o momento de inércia da polia, e o raio da polia foram dados.
O objetivo do enunciado é que determinemos o tempo que o bloco leva pra descer uma distância no plano inclinado. Sacaram?
Bom, como o nosso probleminha envolve tempo, com certeza vamos precisar usar uma daquelas equações horárias de cinemática. Já que a aceleração do bloco deve ser constante, uma boa ideia é usar a “sorvetão”, lembram?
Massa! Mas, a maior dificuldade desse problema é justamente como encontrar a aceleração do bloquinho.
Sempre que tivermos um probleminha envolvendo rodas, discos, polias, e tudo aquilo que gira haha, é uma boa darmos uma pensada na equação abaixo:
onde é o torque resultante sobre o objeto que gira, o seu momento de inércia e sua aceleração angular.
Vamos buscar usar essa expressão pra matar o nosso problema 😊
Passo 2
Bom, temos a seguinte situação descrita no enunciado:
Como vimos no passo anterior, a nossa ideia inicial é usar a equação:
Então, pra começar precisamos determinar o torque resultante sobre a polia.
O torque atuante na polia vem justamente da força com que o fio está tracionado fazendo a polia girar. Ou seja:
Porém do equilíbrio de forças no bloquinho de massa , temos que:
é a componente da força peso na direção do plano inclinado, ou seja:
Logo:
Porém, pelo vínculo geométrico da figura, como o fio é inextensível, o bloquinho, o fio e a polia precisam ter a mesma aceleração linear. Assim, podemos escrever que:
Perfeito!
Reescrevendo nossas equações, vamos ter:
Então:
Logo:
Como foi dado no enunciado, o momento de inércia da polia, vale:
Substituindo, ficamos com:
Logo:
Perfeito galera! Encontramos a aceleração com a qual o bloquinho desce o plano inclinado.
Agora é só partir pras equações horárias.
Passo 3
Já encontramos que:
Assim, podemos usar a equação do “sorvetão”, que comentamos no passo , pra matar esse problema.
Como , e o bloco parte do repouso, vem:
Substituindo a aceleração que encontramos, vamos ter:
Aeeeee! É isso aí pessoal!
Vocês curtiram a solução? Responde Aí!