UFABC – Fundamentos de Mecânica – Lista 3 – Questão 1
Três astronautas, impulsionados por mochilas a jato, empurram e guiam um asteroide de para uma base de manutenção, exercendo as forças mostradas na Fig. 5-29, com , , , e . Determine a aceleração do asteroide
(a) em termos dos vetores unitários e como
(b) um módulo e
(c) um ângulo em relação ao semieixo positivo.
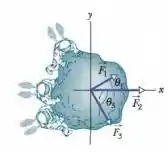
Passo 1
Oi pessoal, a ideia para resolver essa questão é fazer desenho! Então para cada etapa vou fazer od esneho das componentes dos vetores! Vamos lá?
Letra (a):
Bom galera , como a força resultante aplicada ao asteroide é , nós sabemos que a aceleração do asteroide é dada por
Podemos decompor esses vetores em termos dos vetores unitários (componentes vertical e horizontal):
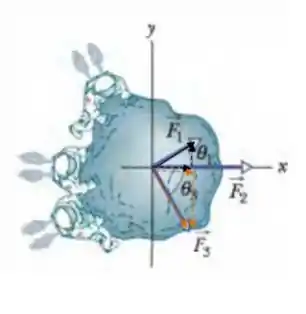
As componentes vertical e horizontal dos vetores e estão representados pelas setas tracejadas (preto e laranja respectivamente). O único vetor que não precosa ser decomposto é o , piis ele está todo ao longo de .
Na notação dos vetores unitários, as forças exercidas pelos astronautas são:
A soma vetorial é ser feita componente a componente (i com i, j com j)!
A aceleração do asteroide é, portanto,
Beleza?
Passo 2
Letra (b):
O módulo de um vetor é
Como calculamos as componentes do vetor aceleração no passo anterior, podemos calcular o módulo da aceleração!
Assim o módulo do vetor aceleração é:
Passo 3
Letra (c):
Podemos achar o ângulo que o vetor faz com o eixo x usando a trigonometria básica! O ângulo do vetor aceleração com o semieixo positivo é o arco tangente da razão entre as componentes e ! Aproveitando o resultado das componentes do passo 1, o ângulo com o eixo horizontal é:
Tranquilo pessoal? É isso!
Espero ter ajudado!