Enunciado das questões (Q6) e (Q7).
Um cilindro uniforme de massa e raio está apoiado num eixo horizontal, podendo girar livremente, sem atrito. Uma corda enrolada no cilindro prende um bloco de massa , que pode deslizar sem atrito sobre um plano inclinado de ângulo , como mostra a figura. O sistema é solto, a partir do repouso, quando está a uma altura acima da horizontal.
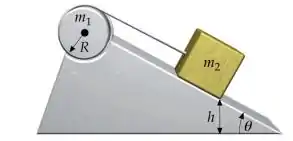
(Q6) [1,0 ponto] A velocidade v com que chega ao plano horizontal é:
Passo 1
POW! Queremos a velocidade do bloco quando ele atingir o chão e uma das formas clássicas de fazer isso é por conservação da energia, principalmente porque sabemos que a energia cinética tem o termo na parada .
Bem, sabemos que no início o bloco só tem energia potencial na altura e a medida que ele desce, essa energia potencial se transforma em energia cinética para o bloco e em energia cinética rotacional para o cilindro ...
Essas energias são...
SHOW! Mas quem é ?
Passo 2
Pow! é a velocidade angular do cilindro! Mas não se preocupe. Ela também se relaciona com a velocidade tangencial do cilindro que é a mesma velocidade que o bloco desce a rampa:
Então...
Se lembrando de agora de que o momento de inércia do cilindro é...
Então agora é só fazer as continhas isolando para ! Bora?
Passo 3
Cortando o que tem de cortar então...
Isolando . Extraindo a raiz quadrada...
Resposta
Letra A.