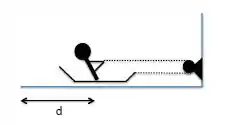
Considere um sistema formado por uma pessoa e um trenó, com massa total , inicialmente em repouso. A pessoa presa ao trenó puxa uma corda ideal com uma força horizontal, constante e de módulo . A corda passa por uma roldana de massa desprezível e está ligada ao trenó, conforme a figura. Considere que o trenó está sobre uma superfície horizontal cujo atrito é desprezível.
a) Desenhe o diagrama de forças que atuam sobre o sistema pessoa + trenó, enquanto a pessoa está puxando a corda;
b) Calcule o tempo necessário que o sistema leva para percorrer uma distância a partir do repouso.
Passo 1
a)
Precisamos apontar as forças sobre o sistema! Primeiro de tudo temos o peso da pessoa+trenó apontando para baixo!
Esse sistema tá em contato com o chão, não tá? Então temos uma normal que aponta para cima.
E agora temos as forças que são exercidas pela corda. A ponta que tá presa no trenó, puxa ele pra direita, então temos uma força, que vamos chamar de , apontando pra direita, beleza?
Já a outra ponta, puxa o moço do trenó pra direita também! Isso por que ao puxar a corda para esquerda o moço é puxado para direita pela terceira lei de Newton! Supondo que a corda é ideal a força sobre o moço também é .
Só pra ficar bem claro, no sistema trenó+moço tem duas forças apontando para direita. E as reações dessas forças ficam onde??? Elas ficam na roldana presa na parede! Sobre essa roldana tem uma força que aponta para esquerda, beleza? A gente só não aponta ela por que o enunciado pede o diagrama de forças sobre o sistema moço+trenó!
O nosso diagrama vai ficar assim:
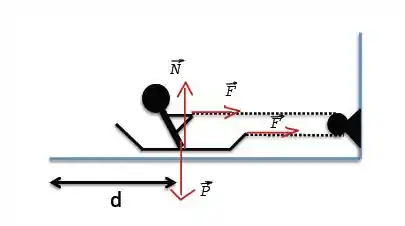
Passo 2
b) Se usarmos a segunda lei de Newton, temos que:
Utilizando somente as forças que estão na horizontal, temos:
Logo:
Como a aceleração é constante, podemos usar a equação da posição do MRUV, lembra?
Mas aqui nós já sabemos de duas coisas:
- é exatamente o deslocamento do trenó, portanto:
- A velocidade inicial é nula, então:
Logo:
Substituindo a aceleração:
Resposta
a)
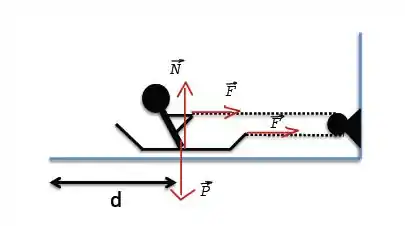
b)