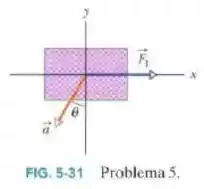
Duas forças agem sobre a caixa de vista de cima na Fig.5-31, mas apenas uma é mostrada. Para , e , determine a segunda força (a) em termos dos vetores unitários e como um (b) módulo e (c) um ângulo em relação ao semieixo positivo.
Passo 1
Primeiro de tudo, esquece aquela força ...
Vamos à Segunda Lei de Newton:
Então, se conhecemos a aceleração e a massa , podemos encontrar a força resultante sobre a caixa.
Sendo o vetor na mesma direção e sentido que o vetor .
Passo 2
Qual a ideia agora?
Bom, existem duas forças agindo sobre a caixa.
A força nós conhecemos, mas a nós não conhecemos:
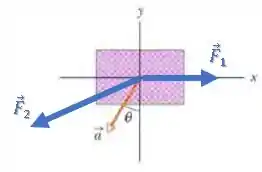
Mas sabemos que a força resultante (conhecida) será a soma delas:
Passo 3
Vamos escrever o vetor Força Resultante em termo de suas componentes.
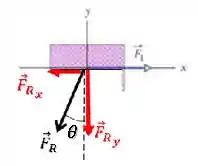
A componente vertical está “colada” no ângulo, então ela será a componente com o cosseno, enquanto a componente na horizontal está “separada” do ângulo, então terá o seno:
Fazendo essas continhas, temos:
Podemos escrever o vetor .
Tanto a componente na horizontal quanto a componente na vertical estão no sentido negativo do eixo, logo:
Passo 4
Agora que já temos a força resultante fica mole!
Voltando à relação de que a é a soma de todas as forças sobre o corpo, temos:
Aqui, temos a opção de trabalhar com cada eixo separadamente, ou então, usar a equação na própria forma vetorial.
Vamos usar direto na forma vetorial!
Como a força (conhecida) está na direção positiva do eixo , o vetor será:
Substituindo os vetores na expressão, temos:
Assim, respondemos a letra (a).
Passo 5
Na letra (b), queremos o módulo da força .
Para achar o módulo de um vetor, basta fecharmos um triângulo retângulo com as suas componentes e aplicarmos Pitágora:
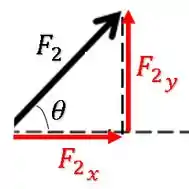
Não se preocupe com desenhar o retângulo na orientação certiiiinha, pois o Pitágoras vai funcionar da mesma maneira.
O importante é que as componentes são perpendiculares.
Assim, temos:
Respondida a letra (b).
Passo 6
Agora na letra (c), queremos um dos ângulos entre a força e o semi-eixo positivo .
Então, primeiro vamos descobrir o ângulo de inclinação de com relação a horizontal.
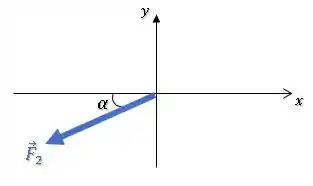
Para achar o ângulo , podemos partir das componentes horizontal e vertical.
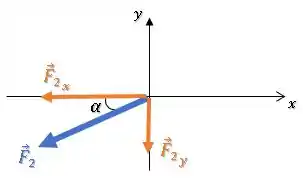
Fechar um triângulo com as componentes horizontal e vertical e usar alguma das identidades trigonométricas:
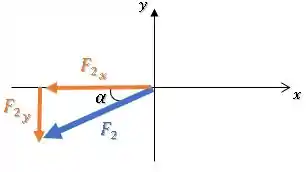
Como não é nenhum dos ângulos notáveis (30°, 45° ou 60°), precisamos usar a calculadora e calcular o arcotangente de , para descobrir o arco cuja tangente vale :
Para obter um dos dois ângulo entre e o semi-eixo positivo , basta somar :
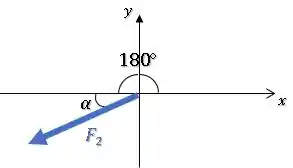
Respondemos a letra (c).
OBS: O segundo ângulo entre e positivo seria.