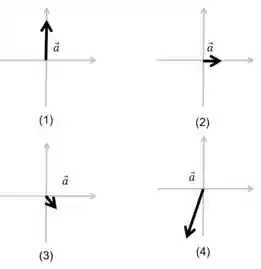
A Fig. 5-24 mostra o diagrama de corpo livre de quatro situações nas quais um objeto, visto de cima, é puxado por várias forças em um piso sem atrito. Em quais dessas situações a aceleração do objeto possui:
(a) uma componente ?
(b) uma componente ?
(c) Em cada situação, indique o sentido de indicando um quadrante ou um sentido ao longo de um eixo. (Isso pode ser feito com alguns cálculos mentais.)
Passo 1
Vamos partir da Segunda Lei de Newton:
Ou seja, a aceleração do corpo está na direção e sentido da força resultante .
Faremos a soma vetorial das forças para chegarmos na força resultante, e encontraremos a aceleração usando a segunda lei de Newton.
Passo 2
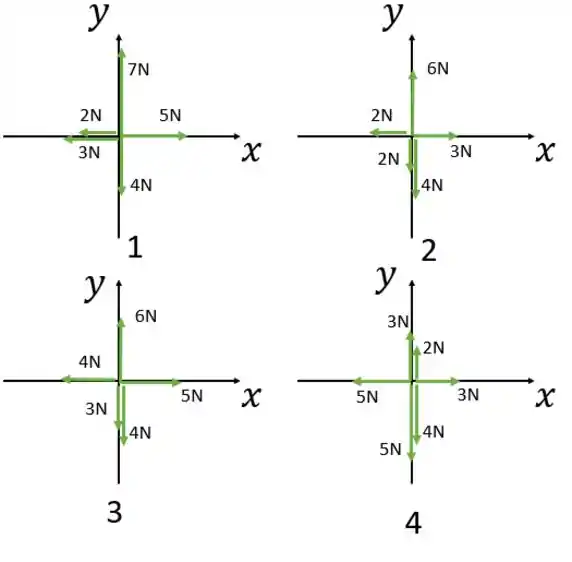
Analisando caso a caso, temos:
Diagrama 1:
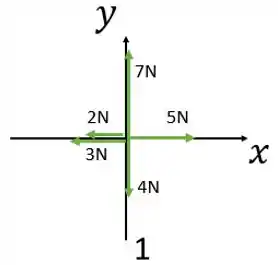
A componente da força resultante na direção do eixo é:
A componente da força resultante na direção do eixo é:
Então, temos que o vetor força resultante será:
Diagrama 2:
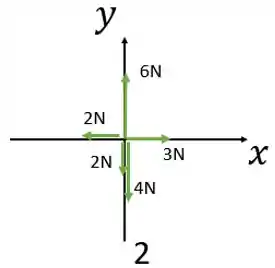
A componente da força resultante na direção do eixo é:
A componente da força resultante na direção do eixo é:
Então, temos que o vetor força resultante será:
Diagrama 3:
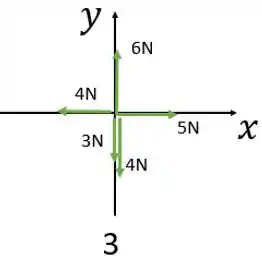
A componente da força resultante na direção do eixo é:
A componente da força resultante na direção do eixo é:
Então, temos que o vetor força resultante será:
Diagrama 4:
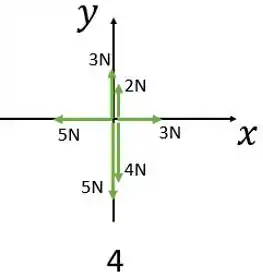
A componente da força resultante na direção do eixo é:
A componente da força resultante na direção do eixo é:
Então, temos que o vetor força resultante será:
Passo 3
Agora que descobrimos os vetores de Força resultante, sabemos a direção do vetor aceleração , pois é o mesmo do vetor Força resultante .
Diagrama 1:
A força resultante apresenta apenas uma componente positiva na direção do eixo , logo:
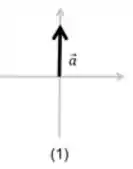
Diagrama 2:
A força resultante apresenta apenas uma componente positiva na direção do eixo , logo:
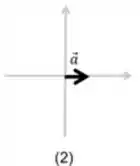
Diagrama 3:
A força resultante apresenta uma componente positiva na direção do eixo e uma componente negativa na direção do eixo , logo:
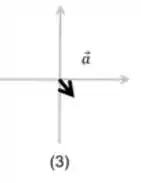
Diagrama 4:
A força resultante apresenta uma componente negativa na direção do eixo e uma componente negativa na direção do eixo , logo:
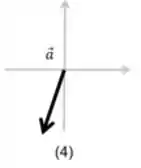
Resposta
- 2, 3 e 4
- 1, 3 e 4