UFSCAR, Sem Campus, Física 1, Listas Física 1 - UFSCAR - Lista 4 - Rotação, rolamento e corpos rígidos, Questão 5b
Uma pessoa permanece de pé numa subida com inclinação de um ângulo com respeito a horizontal. As pernas da pessoa estão separadas entre si por uma distância com um pé na frente do outro. O centro de massa da pessoa está a uma altura do chão, perpendicular a superfície da subida, e no meio das pernas da pessoa. Assuma que o coeficiente de atrito estático entre os pés da pessoa e a subida é grande o suficiente para a pessoa não deslizar.
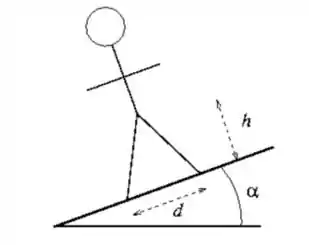
Quanto os pés devem estar separados para que a força normal no pé da frente seja zero? Esta é a situação em que a pessoa começa a rotacionar e cair de costas.
Expresse suas respostas em termos das variáveis do problema.
Passo 1
E aí galera, tudo certo?
Nessa questão temos um problema de estática. Basicamente, uma pessoa está em cima de uma rampa conforme mostrado na imagem:
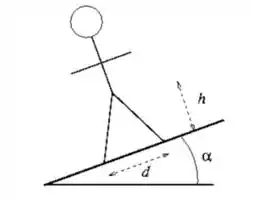
Precisamos determinar qual deve ser a distância pra que a pessoa comece a cair de costas, ou seja, a normal da frente se anule.
Então, no item anterior nós usamos o equilíbrio estático através das equações:
A partir disso, conseguimos encontrar que:
Onde é o pé da frente e o pé de trás da pessoa.
Massa!
Vamos usar a equação que já encontramos pra determinar a condição em que torna nula.
Bora lá!!
Passo 2
Como vimos no passo anterior, temos que:
Queremos que essa normal seja nula, assim:
Logo:
Isolando :
Portanto, a separação entre os pés da pessoa, , para que ela comece a cair de costas, deve ser:
Prontinho galera! É isso aí!
Matamos mais uma questão 😊