UFSCAR, Sem Campus, Física 1, Listas Física 1 - UFSCAR - Lista 4 - Rotação, rolamento e corpos rígidos, Questão 5a
Uma pessoa permanece de pé numa subida com inclinação de um ângulo com respeito a horizontal. As pernas da pessoa estão separadas entre si por uma distância com um pé na frente do outro. O centro de massa da pessoa está a uma altura do chão, perpendicular a superfície da subida, e no meio das pernas da pessoa. Assuma que o coeficiente de atrito estático entre os pés da pessoa e a subida é grande o suficiente para a pessoa não deslizar.
Quais são as magnitudes das forças normais em cada pé? Elas são diferentes para cada pé.
Expresse suas respostas em termos das variáveis do problema
Passo 1
Oiii, tudo bem pessoal?
Nessa questão temos um problema de estática. Basicamente, uma pessoa está em cima de uma rampa conforme mostrado na imagem:
Precisamos determinar a normal em cada um dos pés da pessoa. O enunciado faz questão de frisar que elas terão valores diferentes, beleza?
Alguma ideia de como podemos fazer isso?
Então gente, precisamos sempre ter em mente que se um corpo está em situação de equilíbrio estático, podemos afirmar duas coisas:
Sendo assim, vamos começar identificando as forças que estão atuando no corpo através do diagrama de corpo livre, e depois escolhemos um ponto conveniente pra usar que .
Vamo nessa!
Passo 2
Bom, vamos começar pelo DCL. Atuam na pessoa: duas normais e duas forças de atrito nos seus pés, e uma força peso no seu centro de massa. Assim:
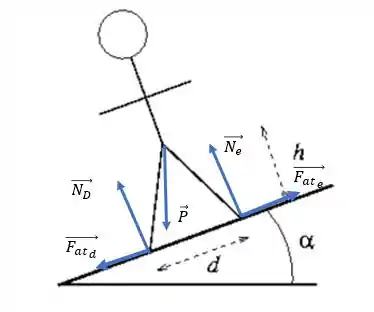
Massa!
Agora, vamos decompor a força peso. Isso vai nos ajudar um pouco ao calcularmos os momentos e também ao escrevermos as equações de equilíbrio de forças.
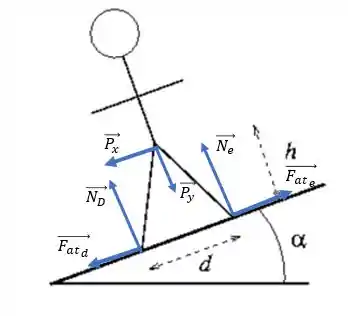
Decompondo a força peso, teremos:
Perfeito!
.
Passo 3
Precisamos então escolher um ponto conveniente pra usarmos a equação dos momentos.
Se escolhermos o pé direito, excluímos do cálculo do momento as forças e . Vamos fazer isso!
Logo, isolando a normal :
Muito bom! Pra calcular podemos usar raciocínio análogo, ou apelar pro equilíbrio de forças na vertical.
Escrevendo a equação de forças, vamos ter que:
Logo:
Prontinho! De fato, as normais são diferentes 😊
É isso galerinha, obrigado pela atenlão!!