Um acelerômetro simples é construído suspendendo-se um corpo de massa por um fio de tamanho que está ligado ao teto do carro. Quando o carro acelera, o fio faz ângulo constante com a vertical.
(a) Desenhe o diagrama de forças atuando no corpo.
(b) Escreva as equações de movimento para o corpo.
(c) Supondo que o fio tenha massa desprezível comparada com , mostre que a expressão da aceleração é função de e que é independente de e .
(d) Se o ângulo medido é , calcule a aceleração do carro.
Dados: , e
Passo 1
a) Fazendo o diagrama do corpo, vamos ter isso aqui:
Passo 2
b) Agora vamos dividir em eixo e eixo .
Passo 3
c) Agora que já montamos as equações para cada eixo, vamos dividir uma pela outra e isolar o nosso (assim ele não vai depender da tração e nem da masssa ).
Passo 4
d) Agora é só substituir os valores e partir pro abraço !
Resposta
a) 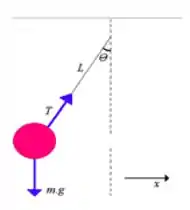
b) ;
c)
d)