Na figura a massa do bloco é e o ângulo é . Determine:
a tensão na corda;
Passo 1
E aí gente bonita, como vocês estão?
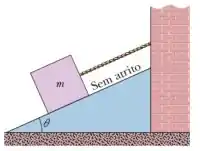
Nessa questão temos um arranjo relativamente simples, de um bloquinho apoiado em um plano inclinado de e preso a uma corda por um dos lados, como mostrado na figura abaixo:
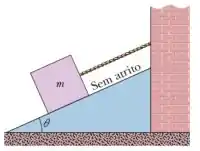
Nesse primeiro item precisamos determinar qual a tensão na corda, dado que o bloco está em repouso (pois não tem como o fio esticar mais do que o seu comprimento natural).
Para fazer isso precisamos avaliar o diagrama de forças do bloco, então vamos começar desenhando e decompondo as forças, para depois escrever as equações do equilíbrio.
Vem comigo!
Passo 2
Bom, vamos começar desenhando as forças que atuam no bloquinho. São elas: a tração da corda, a força peso que será decomposta em (direção do plano) e (direção perpendicular ao plano), e a força normal entre o bloco e a superfície de contato.
Daí, temos:
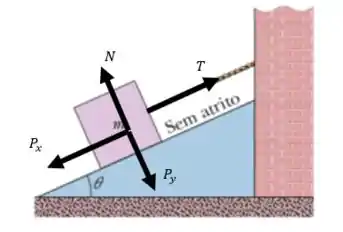
Vamos então decompor a força Peso para encontrar e :
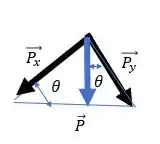
Logo:
Excelente!
Passo 3
Agora vamos escrever a equação de equilíbrio na horizontal:
Como e , temos:
Prontinho! Até a próxima gente 😊