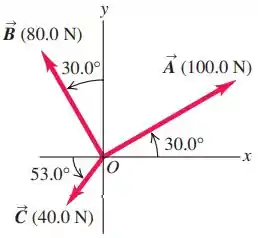
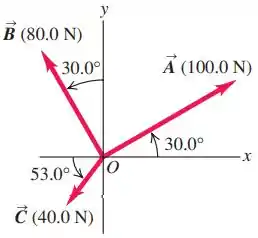
Três cordas horizontais puxam uma grande pedra presa ao chão, produzindo as forças vetoriais: mostradas na figura abaixo. Encontre a magnitude e a direção de uma quarta força na pedra que fará com que fará com que a soma vetorial das quatro forças seja zero.

Primeiro vamos decompor os vetores em relação ao eixo x

Lembrando que caso a força esteja apontando para o lado negativo do eixo , a intensidade da força será negativa.

Agora vamos fazer o mesmo procedimento só que agora em relação ao eixo :

Novamente, caso a força esteja apontando para o lado negativo do eixo , sua intensidade será negativa.

Como já decompomos todos os vetores chegou a hora de encontrarmos o quarto vetor. Somando todas as componentes de cada vetor em obtemos que :

Vamos novamente utilizar o mesmo procedimento do passo anterior só que agora o eixo em questão é o :

Bommmm xuxus, já temos as componentes do vetor , entretanto, estamos interessados no módulo desse vetor, como poderemos encontrar???

Basta que apliquemos o Teorema de Pitágoras:

Portanto,

Obaaa até quem fim achamos a intensidade desse vetor força, agora só resta encontrar sua angulação.

Para encontrar o ângulo que essa corda faz com o eixo é só utilizar a expressão da tangente:

Para encontrar de fato o ângulo, vamos utilizar o com o auxílio de uma calculadora encontramos que o ângulo é em relação ao eixo x.

Sabemos o ângulo e que esse vetor se encontra no terceiro quadrante devido aos valores negativos tanto da componente x quanto da componente y.

Se liga só: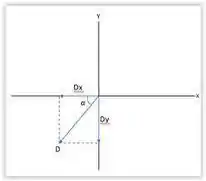

Conseguimossss finalizar a questão. Vocês são incríveis 😊