Uma esfera com uma massa de está suspensa por uma corda. Uma brisa horizontal constante empurra a esfera (com velocidade constante) de tal forma que a corda faz um ângulo de com a vertical. Determine:
A tensão da corda;
Passo 1
Fala aí gente, tudo beleza?
Nessa questão temos uma esfera pendurada por uma corda, que está inclinada em relação à vertical em , pois há uma força lateral devido à uma brisa atuando na esfera.
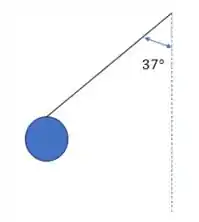
Queremos determinar a tensão na corda que segura a bola.

Para fazer isso, vamos desenhar as forças que atuam na esfera para depois escrever as equações de equilíbrio, beleza?
Passo 2
Bom, na esfera atuam a tração do fio, a força peso da esfera e a força lateral da brisa.
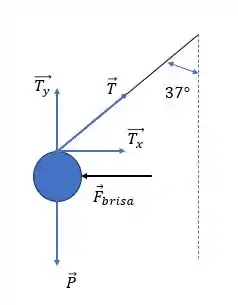
Agora vamos calcular essas componentes da tração:
Esse ângulo de é justamente o menor ângulo do triângulo pitagórico. Daí:
Portanto:
Massa!
Passo 3
Agora, vamos escrever as equações de equilíbrio.
Na vertical, temos:
Daí, isolando a tração, vem que:
Portanto:
Logo:
Prontinho galera, obrigado pela atenção de vocês!