UFSCAR, Sorocaba, Física 1, Listas de Física 1 - UFSCAR (Sorocaba) - Lista 3, Questão 5b
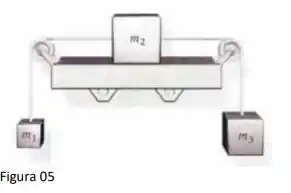
Uma caixa de massa 𝑚2 = 3,5𝑘𝑔 está sobre uma estante horizontal sem atrito e presa por fios a caixas de massa 𝑚1 = 1,5𝑘𝑔 e 𝑚3 = 2,5𝑘𝑔, conforme figura 5. As duas polias são sem atrito e sem massa. O sistema é solto do repouso. Após a largada, encontre
(b) a tensão em cada fio
Passo 1
Eaew, belezinha?
Temos uma caixa de massa 𝑚2 = 3,5𝑘𝑔 que está sobre uma estante horizontal sem atrito e presa por fios a caixas de massa 𝑚1 = 1,5𝑘𝑔 e 𝑚3 = 2,5𝑘𝑔. As duas polias são sem atrito e sem massa. O sistema é solto do repouso. Foi pedido para calcularmos a a tensão em cada fio
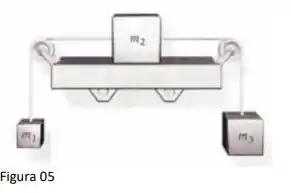
Primeiro vamos identificar as forças presentes em cada caixa e lembrar que o módulo da aceleração de cada caixa é igual, a partir daí conseguiremos calcular o valor desta aceleração, e então a tensão em cada fio. Então vamos lá!
Passo 2
Primeiro vamos observar as forças envolvidas
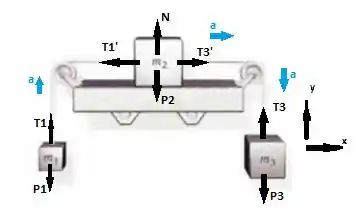
Note que a normal N na caixa 2 se anula com a sua força de peso. Note também que T1=T1’ e T3=T3’.
Passo 3
Vamos escrever a força resultante para cada caixa:
Caixa 1:
Caixa 2:
Caixa 3:
Passo 4
Isolando T1 e T3 e substituindo na equação da força resultante da caixa 2, temos
isolando a aceleração
usando
Passo 5
Substituindo nas relações para as tensões:
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta