USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e Energia, Questão 35
Um bloco de massa é puxado ao longo de uma superfície, lisa e horizontal, por uma corda de massa sobre a qual se exerce uma força horizontal . Determine as acelerações do bloco e da corda e a força exercida pela corda sobre o bloco. Qual é o valor de se desprezarmos em confronto com ?
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar a aceleração do bloco e da corda, considerando que a corda tá puxando esse bloco por uma superfície lisa, sem atrito. Ele nos disse que a corda exerce uma força horizontal sobre o bloco. Como não há movimento na vertical, essa é a única força que nós vamos considerar.
Além disso, a corda e o bloco se movimentam juntos, então podemos considerar como a aceleração do sistema, pois o bloco e a corda terão a mesma aceleração.
Assim, vamos usar a equação fundamental da dinâmica para calcular a aceleração:
Em seguida, vamos determinar a força de tração exercida pela corda sobre o bloco, considerando as forças que estão agindo nela e usando a mesma equação.
Vamos lá!
Passo 2
Usando , onde é a massa do bloco e a massa da corda, temos:
Isolando :
E temos nossa aceleração.
Passo 3
Para saber o valor da tração , vamos avaliar as forças que atuam sobre a corda:
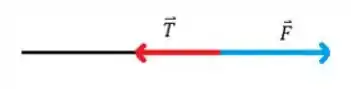
Pela segunda Lei de Newton, temos:
Onde é a força resultante do sistema. Então, somando as forças do DCL, temos:
Substituindo , encontrado no passo anterior, vamos ter:
Isolando :
Simplificando:
Passo 4
Agora vamos descobrir o valor de se desprezarmos em confronto com . Considerando , teríamos:
E simplificando:
Valeu, galera! Até a próxima! 😉