Um objeto de massa é puxado para cima, na vertical, por meio de um fio ideal. Sabe-se que a tensão máxima que o fio suporta, sem se romper, é (com ). Qual é a maior aceleração que o corpo pode ter sem que o fio arrebente?
(a)
(b)
(c)
(d)
(e)
(f)
Passo 1
A situação é a seguinte:
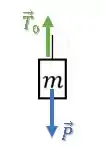
Esse corpo está sendo puxado para cima, e queremos saber qual a maior aceleração que o corpo pode sofrer sem que o fio arrebente.
Concorda comigo que quanto maior a força de tração que puxamos o bloco, maior a aceleração que o bloco vai ter?
Isso mesmo né!
Então, devemos puxar o bloco com a maior força possível, e essa maior força possível será o limite de tensão que o fio suporta .
Passo 2
Agora, para achar a maior aceleração possível, vamos relacionar força e aceleração a partir da Segunda Lei de Newton:
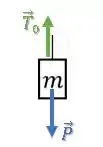
Como a aceleração está para cima, vamos considerar esse sentido positivo para as forças:
Mas sabemos que a força peso é dada pela massa vezes a gravidade , então:
Pronto, essa é a maior aceleração possível para o bloco sem que o fio arrebente.
Resposta
Letra (d)